RBSE Solutions for Class 12 Physics Chapter 4 विद्युत धारिता

हेलो स्टूडेंट्स, यहां हमने राजस्थान बोर्ड कक्षा 12वीं की भौतिक विज्ञान सॉल्यूशंस को दिया हैं। यह solutions स्टूडेंट के परीक्षा में बहुत सहायक होंगे | Student RBSE solutions for Class 12 Physics Chapter 4 विद्युत धारिता pdf Download करे| RBSE solutions for Class 12 Physics Chapter 4 विद्युत धारिता notes will help you.

राजस्थान बोर्ड कक्षा 12 physics के सभी प्रश्न के उत्तर को विस्तार से समझाया गया है जिससे स्टूडेंट को आसानी से समझ आ जाये | सभी प्रश्न उत्तर Latest Rajasthan board Class 12 physics syllabus के आधार पर बताये गए है | यह सोलूशन्स को हिंदी मेडिअम के स्टूडेंट्स को ध्यान में रख कर बनाये है |

Rajasthan Board RBSE Class 12 Physics Chapter 4 विद्युत धारिता

RBSE Class 12 Physics Chapter 4 पाठ्य पुस्तक के प्रश्न एवं उत्तर

RBSE Class 12 Physics Chapter 4 बहुचयनात्मक प्रश्न

प्रश्न 1.
किसी गोलीय चालक की धारिता का मान समानुपाती होता है
(अ) C ∝ R
(ब) C ∝ R²
(स) C ∝ R^-2
(द) C ∝ R^-1
उत्तर:
(अ) C ∝ R
गोलीय चालक की धारिता C = 2πμ₀R
C ∝ R

प्रश्न 2.
दिये गये चित्र में बिन्दु A तथा B के मध्य तुल्य धारिता का मान होगा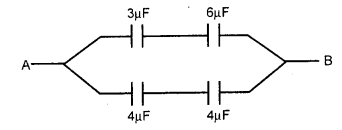

(अ) 2μF
(ब) 4μF
(स) 25μF
(द) 3μF
उत्तर:
(ब) 4μF


= 2μF + 2μF
= 4μF

प्रश्न 3.
एक आवेशित संधारित्र की दोनों प्लेटों को एक तार से जोड़ दिया जाये तब
(अ) विभव अनन्त हो जायेगा।
(ब) आवेश अनन्त हो जायेगा
(स) आवेश पूर्व मान का दुगुना हो जायेगा
(द) संधारित्र निरावेशित हो जायेगा।
उत्तर:
(द) संधारित्र निरावेशित हो जायेगा।
संधारित्र की दोनों प्लेटों को तार से जोड़ने पर चालन के कारण संधारित्र निरावेशित हो जायेगा।

प्रश्न 4.
दिये गये चित्र में संयोजित संधारित्रों के लिये बिन्दु A तथा B के मध्य तुल्य धारिता का मान होगा—-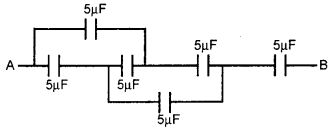

(अ) 5μF
(ब) 2.5μF
(स) 10μF
(द) 20μF
उत्तर:
(ब) 2.5μF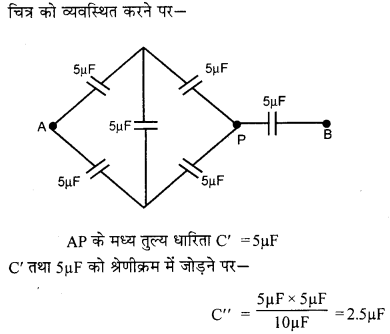

प्रश्न 5.
दो गोलाकार चालकों की त्रिज्याओं का अनुपात 1 : 2 है, तो। उनकी धारिताओं का अनुपात होगा
(अ) 4: 1
(ब) 1 : 4
(स) 1 : 2
(द) 2 : 1
उत्तर:
(ब) 1 : 4
गोलीय चालक के लिये C ∝ R
[latex]frac{C_{1}}{C_{2}}=frac{R_{1}}{R_{2}}=frac{1}{2}[/latex]

प्रश्न 6.
चित्र के अनुसार एक समान्तर प्लेट संधारित्र की प्लेटों के मध्य आधे भाग में किसी परावैद्युत पदार्थ जिसका परावैद्युतांक ε_r है, सरकाया जाता है। यदि संधारित्र की प्रारम्भिक धारिता C हो तब नवीन धारिता का मान होगा।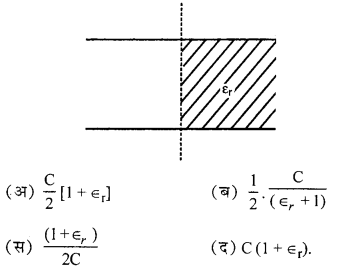

उत्तर:
(अ)

प्रश्न 7.
समान त्रिज्या तथा समान आवेश की पारे की आठ बूंदें परस्पर मिलकर एक बड़ी बूंद बनाती हैं। बड़ी बूंद की धारिता प्रत्येक छोटी बूंद की धारिता की तुलना में होगी
(अ) 2 गुना
(ब) 8 गुना
(स) 4 गुना
(द) 16 गुना
उत्तर:
(अ) 2 गुना
बड़ी बूंद का आयतन = 8 × छोटी बूंद का आयतन
[latex]frac{4}{3}[/latex]πR³ = 8 × [latex]frac{4}{3}[/latex]πr³
R = 2r
छोटी बूंद की धारिता G = 4πε₀r
तथा बड़ी बूंद की त्रिज्या C₂ =4πε₀R
[latex]frac{C_{1}}{C_{2}}=frac{r}{R}=frac{r}{2 r}[/latex]
अर्थात् दोगुनी हो जायेगी

प्रश्न 8.
एक संधारित्र की धारिता C है। इसे v विभवान्तर तक आवेशित किया गया है। यदि अब इसे प्रतिरोध से सम्बन्धित कर दिया जाये तब ऊर्जा क्षय की मात्रा होगी–
(अ) CV²
(ब) [latex]frac{1}{2}[/latex] CV²
(स) [latex]frac{1}{3}[/latex] CV²
(द) [latex]frac{1}{2}[/latex] QV²
उत्तर:
(ब) [latex]frac{1}{2}[/latex] CV²
ऊर्जा क्षय = संधारित्र में संचित ऊर्जा
[latex]frac{1}{2}[/latex] CV²

प्रश्न 9.
यदि एक संधारित्र को आवेश Q देने पर संग्रहीत ऊर्जा W है। आवेश दुगुना करने पर संग्रहीत ऊर्जा होगी
(अ) 2w
(ब) 4W
(स) 8w
(द) [latex]frac{1}{2}[/latex] w
उत्तर:
(ब) 4W

प्रश्न 10.
3μF व 5μF के दो गोलों को क्रमशः 300V तथा 500V तक आवेशित कर जोड़ दिया जाता है। उभयनिष्ठ विभव होगा—
(अ) 400V
(ब) 375V
(स) 425V
(द) 350V
उत्तर:
(स) 425V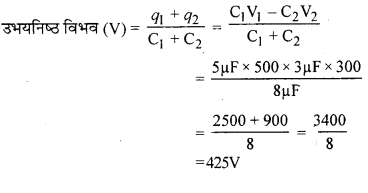

प्रश्न 11.
एक आवेशित समान्तर प्लेट संधारित्र की प्लेटों के मध्य स्थितिज ऊर्जा U₀ है यदि एक ε_r परावैद्युतांक वाली पट्टिका मध्य में रख दी जाये तब नवीन स्थितिज ऊर्जा होगी—
(अ) [latex]frac{mathrm{U}_{0}}{epsilon_{r}}[/latex]
(ब) U₀ε_r²
(स) [latex]frac{mathrm{U}_{0}}{epsilon_{r}^{2}}[/latex]
(द) U₀
उत्तर:
(अ) [latex]frac{mathrm{U}_{0}}{epsilon_{r}}[/latex]
ऊर्जा ε_r गुना कम हो जायेगी।
∴ U = [latex]frac{mathrm{U}_{0}}{epsilon_{r}}[/latex]

प्रश्न 12.
चित्र में दिखाये गये परिपथ में 4.5uF वाले संधारित्र पर विभवान्तर है।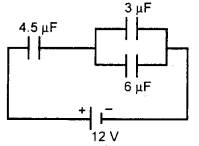

(अ) [latex]frac{8}{3}[/latex] V
(ब) 4V
(स) 6V
(द) 8V
उत्तर:
(द) 8V

प्रश्न 13.
चित्र में दिखाये गये परिपथ में A व B के मध्य तुल्य धारिता होगी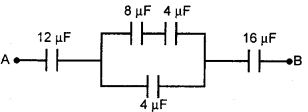

(अ) 1F
(ब) 9F
(स) 1.5F
(द) 1/3F
उत्तर:
(अ) 1F

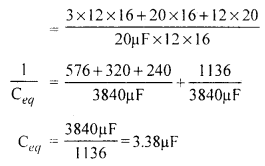
RBSE Class 12 Physics Chapter 4 अति लघूत्तरात्मक प्रश्न

प्रश्न 1.
एक समान्तर प्लेट संधारित्र की एक प्लेट का क्षेत्रफल आधा कर दिया जाये तो क्या यह युक्ति संधारित्र का कार्य करेगी ?
उत्तर;
नहीं, क्योंकि दोनों प्लेटों पर आवेश असमान हो जायेगा।

प्रश्न 2.
तीन संधारित्रों जिनके प्रत्येक की धारिता 6μF है, के संयोजनों से प्राप्त अधिकतम व न्यूनतम धारिताओं का मान क्या होगा ?
उत्तर:
(i) अधिकतम धारिता के लिये तीनों को समान्तर क्रम में जोड़ा जाता है।
∴ C_max = C₁ + C₂ + C₃ = 6μF + 6μF + 6μF = 18μF
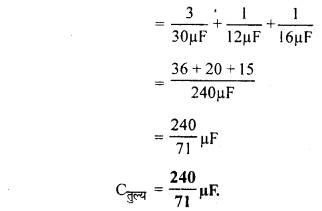
(ii) न्यूनतम धारिता के लिये तीनों को श्रेणीक्रम में संयोजित करते हैं।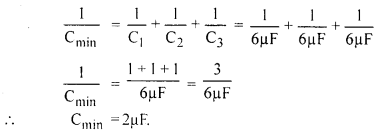

प्रश्न 3.
किसी चालक की धारिता का मान किन कारकों पर निर्भर करता है ?
उत्तर:
किसी चालक की धारिता का मान चालक के अनुप्रस्थ काट के क्षेत्रफल तथा उसके चारों ओर के माध्यम पर निर्भर करता है।

प्रश्न 4.
पृथ्वी को गोलीय चालक मानने पर पृथ्वी की धारिता कितनी होती है ?
उत्तर:
गोलीय चालक की धारिता (C)
=4πε₀R
= [latex]frac{6 cdot 4 times 10^{6}}{9 times 10^{9}}[/latex] = 711μF

प्रश्न 5.
आवेशित समान्तर प्लेट संधारित्र की प्लेटों के मध्य परिणामी विद्युत् क्षेत्र कितना होता है जबकि प्लेटों पर पृष्ठ आवेश घनत्व σ है ?
उत्तर:
परिणामी विद्युत क्षेत्र E = [latex]frac{sigma}{varepsilon_{0}}[/latex]

प्रश्न 6.
यदि समान धारिता C के n संधारित्र श्रेणीक्रम में जोड़े जाये तब तुल्य धारिता कितनी होगी ?
उत्तर:
C_{परिणामी} = [latex]frac{C}{n}[/latex]

प्रश्न 7.
समान्तर प्लेट संधारित्र की प्लेटों के मध्य ऊर्जा घनत्व को सूत्र लिखिये।
उत्तर:
u = [latex]frac{mathrm{U}}{mathrm{V}}=frac{1}{2}[/latex] ε₀E² जहाँ E = विद्युत क्षेत्र

प्रश्न 8.
ऊर्जा घनत्व का मात्रक लिखिये।
उत्तर:

प्रश्न 9.
दो संधारित्र जिनकी धारितायें C₁ व C₂ हैं। यदि उन्हें समान आवेश दिये जायें तब उनमें एकत्रित स्थिर विद्युत स्थितिज ऊर्जाओं का अनुपात लिखिये।
उत्तर: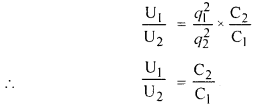

प्रश्न 10.
ऐसा चालक बताइये जिसको लगभग असीमित (अनन्त) आवेश दिया जा सकता हो।
उत्तर:
पृथ्वी, क्योंकि इसकी धारिता अधिक होती है।

प्रश्न 11.
किसी आवेशित संधारित्र की ऊर्जा किस रूप में कहाँ संचित रहती है ?
उत्तर:
संधारित्र की ऊर्जा विद्युत ऊर्जा के रूप में प्लेटों के मध्य संचित होती है।

प्रश्न 12.
किसी आवेशित संधारित्र पर नैट विद्युत आवेश कितना होता है ?
उत्तर:
0 (शून्य)

प्रश्न 13.
किसी समान्तर प्लेट संधारित्र की प्लेटों के सम्पूर्ण स्थान में कोई परावैद्युत भरने से उसकी धारिता 5 गुनी हो जाती है। परावैद्युत का पराविद्युतांक क्या है ?
उत्तर:
ε_r = [latex]frac{C_{m}}{C}=frac{5 C}{C}[/latex] = 5

प्रश्न 14.
संधारित्र का मूल उपयोग क्या है ?
उत्तर:
विद्युत आवेश तथा विद्युत ऊर्जा की बड़ी मात्रा को संचित करने के लिये।

प्रश्न 15.
एक समान्तर प्लेट संधारित्र की प्लेटों के मध्य की दूरी d है। यदि d/2 मोटाई की कोई धात्विक प्लेट संधारित्र के प्लेटों के मध्य रख दी जाये तब धारिता पर क्या प्रभाव पड़ेगा ?
उत्तर:

अर्थात् धारिता दोगुनी हो जायेगी।

प्रश्न 16.
24μF धारिता के संधारित्र को आवेशित करने में कितना कार्य करना पड़ेगा जबकि प्लेटों के मध्य विभवान्तर 500V
उत्तर:
कार्य (W) = q.V
W = 24 × 10^-6 × 500 × 500
= 6J

प्रश्न 17.
यदि आपको कम धारिता के संधारित्र दिये हैं तो | इनसे अधिक धारिता किस प्रकार प्राप्त करेंगे ?
उत्तर:
दिये गये संधारित्रों को समान्तर क्रम में जोड़ने पर।

प्रश्न 18.
2μF धारिता वाले दो संधारित्रों को श्रेणीक्रम में जोड़ने पर तुल्य धारिता कितनी होगी ?
उत्तर: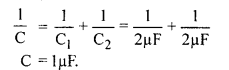

प्रश्न 19.
एक समान्तर प्लेट संधारित्र को तेल में डुबोने से । उसकी धारिता पर क्या प्रभाव पड़ेगा ? तेल का परावैद्युतॉक 2 है।
उत्तर:
किसी माध्यम में धारिता C = KC₀, K = 2
∴ धारिता दोगुनी हो जायेगी।

प्रश्न 20.
वृत्ताकार समान्तर प्लेट संधारित्र की त्रिज्या है। प्लेटों के मध्य हवा भरी है। यदि संधारित्र की धारिता R त्रिज्या के गोले की धारिता के बराबर है तब प्लेटों के मध्य दूरी बताइये।
उत्तर:

RBSE Class 12 Physics Chapter 4 लघूत्तरात्मक प्रश्न

प्रश्न 1.
चालक एवं विद्युतरोधी को उदाहरण सहित समझाइये।
उत्तर:
चालक एवं विद्युतरोधी (Conductor and Insulator)
प्रकृति में पाये जाने वाले अधिकांश पदार्थों को विद्युत धारा के प्रवाह के आधार पर दो भागों में बाँटा जा सकता है-(i) चालक, (ii) अचालक या विद्युतरोधी।
“वह पदार्थ जो आवेश को ले जाने या आवेश को एक स्थान से दूसरे स्थान तक ले जाने के लिए प्रयोग किया जाता है, चालक कहलाता है।” चाँदी सर्वोत्तम चालक है, इसके अलावा सभी धातुएँ चालक की श्रेणी में आती हैं, जैसे ताँबा, लोहा, ऐलुमिनियम, पारा आदि। पृथ्वी भी विद्युत की अच्छी सुचालक (good conductor) है और मानव शरीर भी विद्युत का सुचालक है। सभी लवणों, अम्लों एवं क्षारों के जलीय घोल (water soluble salts, acids and bases) विद्युत के सुचालक होते हैं। इन घोलों में मौजूद आयन आवेश वाहक (charge carriers) का कार्य करते हैं।

धातुओं में मौजूद मुक्त इलेक्ट्रॉन (free electrons) आवेश वाहक का कार्य करते हैं। मुक्त इलेक्ट्रॉन परमाणुओं की सबसे बाहरी कक्षा के इलेक्ट्रॉन होते हैं जो थोड़ी भी ऊर्जा पाकर संगत परमाणु को छोड़कर चालक की परिसीमाओं (boundary) के अन्दर कहीं भी घूम सकते हैं। लेकिन चालक को छोड़कर नहीं जा सकते हैं। इन मुक्त (free) इलेक्ट्रॉनों की तुलना किसी बर्तन में बन्द गैस के अणुओं से की जा सकती है, अतः इनके समूह को इलेक्ट्रॉन गैस भी कह सकते हैं।

विद्युतरोधी या अचालक (Insulators)-अचालक वे पदार्थ होते हैं जिनसे होकर विद्युत प्रवाह नहीं हो सकता है। अचालकों के सामान्य उदाहरण काँच, रबर, प्लास्टिक, एबोनाईट, अभ्रक, मोम आदि हैं। इन पदार्थों में नगण्य संख्या में मुक्त इलेक्ट्रॉन होते हैं। दूसरे शब्दों में यह कह सकते हैं कि इन पदार्थों के परमाणुओं में सभी इलेक्ट्रॉन बद्ध इलेक्ट्रॉन (bound electrons) होते हैं और वे मुक्त रूप से गति नहीं कर सकते हैं। चूँकि अचालकों में मुक्त रूप से विचरण (movable) करने वाले आवेश नहीं होते हैं इसलिए इनसे होकर विद्युत का चालन सम्भव नहीं होता है।

यह स्मरणीय तथ्य है कि अचालकों को ही परावैद्युत (dielectric) पदार्थ भी कहते हैं। स्वाभाविक है कि परावैद्युत माध्यमों में भी विद्युत प्रवाह सम्भव नहीं है लेकिन बाहरी विद्युत क्षेत्र (external electric field) में रखने पर इनकी सतह पर प्रेरित आवेश एकत्र हो जाता है। इस प्रकार हम परावैद्युत पदार्थ की परिभाषा निम्न प्रकार कर सकते हैं, “वे अचालक पदार्थ जो चालन के बिना विद्युत प्रभाव का प्रदर्शन करते हैं, परावैद्युत पदार्थ कहलाते हैं।”

प्रश्न 2.
ध्रुवीय तथा अधुवीय परावैद्युत में अन्तर स्पष्ट कीजिये।
उत्तर:
मुक्त एवं बद्ध आवेश (Free and Bound Charges)
प्रत्येक पदार्थ परमाणु से मिलकर बना होता है। परमाणु की संरचना में एक भाग नाभिक होता है जिसके अन्दर प्रोटॉन तथा न्यूट्रॉन रहते हैं तथा नाभिक के चारों ओर इलेक्ट्रॉन वृत्तीय कक्षा में घूमते रहते हैं।
नाभिक के परित: निश्चित कक्षाओं में इलेक्ट्रॉन बिना कोई ऊर्जा नष्ट किये गतिशील रहते हैं। इलेक्ट्रॉन पर – 1.6 × 10^-19 कूलॉम आवेश होता है और इसका द्रव्यमान 9.1 × 10^-31 kg होता है। परमाणु विद्युत उदासीन (electrically neutral) होता है।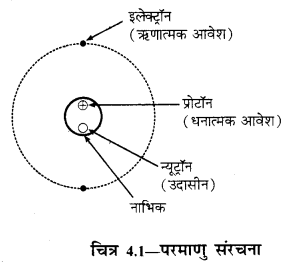

अतः नाभिक में जितने प्रोटॉन होते हैं उतने ही इलेक्ट्रॉन नाभिक के परितः चक्कर लगाते हैं। जो इलेक्ट्रॉन नाभिक के समीप वाली कक्षाओं में होते हैं उन पर नाभिक का नियन्त्रण अधिक होता है, इन्हें सम्बद्ध या बद्ध इलेक्ट्रॉन (bound electron) कहते हैं। इन इलेक्ट्रॉनों को आसानी से नाभिक से अलग नहीं किया जा सकता है। जैसे-जैसे इलेक्ट्रॉन नाभिक से दूर जाते हैं, नाभिक का इलेक्ट्रॉन पर से नियन्त्रण कम होता जाता है। तथा अन्तिम कक्षा वाले इलेक्ट्रॉनों पर नाभिक का नियन्त्रण सबसे कम होता है। इन इलेक्ट्रॉनों को मुक्त इलेक्ट्रॉन (free electron) कहते हैं। क्योंकि थोड़ी-सी ऊर्जा देने पर इन इलेक्ट्रॉनों को संगत परमाणुओं से अलग किया जा सकता है।

कुचालक पदार्थ के परमाणु की बाह्यतम कक्षा के इलेक्ट्रॉनों पर नाभिक का आकर्षण बल प्रबल होता है अत: इनके सभी इलेक्ट्रॉन बद्ध अवस्था में होते हैं। इनका स्वतन्त्र रूप से विचरण सम्भव नहीं हो पाता है। अतः इन पदार्थों में धारा का चालन नहीं होता है।

प्रश्न 3.
किसी गोलीय चालक की धारिता का व्यंजक स्थापित कीजिये।
उत्तर:
विलगित गोलीय चालक की धारिता (Capacitance of an Isolated Spherical Conductor)
माना R त्रिज्या का एक गोलाकार चालक K परावैद्युतॉक वाले माध्यम में रखा है। जब इस गोले को +q आवेश दिया जाता है तो यह आवेश गोले के पृष्ठ पर समान रूप से वितरित हो जाता है और फलस्वरूप गोले के पृष्ठ पर विभव Vउत्पन्न हो जाता है। गोले का पृष्ठ समविभव पृष्ठ (equi-potential surface) की भाँति व्यवहार करता है। अतः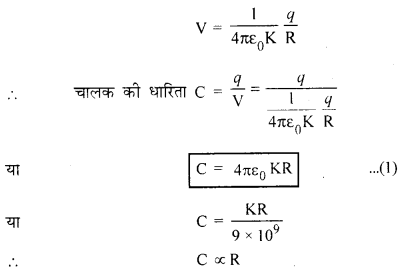

अर्थात् किसी गोलाकार चालक की धारिता उसकी त्रिज्या के अनुक्रमानुपाती होती है।
यदि गोलीय चालक, किसी परावैद्युत माध्यम में स्थित हो जिसको परावैद्युतॉक ६, हो तो उसकी धारिता
C_m = [latex]frac{q}{mathrm{V}}[/latex] = 4πε₀ε_rR
C_m = 4πε₀Rε_r
∴ [latex]frac{C_{m}}{C}[/latex] = ε_r
अत: माध्यम का परावैद्युतॉक माध्यम की विद्युत धारिता एवं वायु (निर्वात्) की विद्युत धारिता के अनुपात के बराबर होती है।

प्रश्न 4.
एक आवेशित समान्तर प्लेट संधारित्र की प्लेटों को निकट लाने पर उसकी प्लेटों के मध्य विभवान्तर पर क्या प्रभाव पड़ेगा ? जबकि आवेश नियत रखा जाता है। समझाइये।
उत्तर:
q = CV ⇒ V = [latex]frac{q}{C}[/latex]
अर्थात् V ∝ [latex]frac{1}{C}[/latex] होती है जब आवेश नियत रहता है।
निकट जाने पर d का मान कम होता है लेकिन धारिता के सूत्र C = ε₀A/d के अनुसार C का मान बढ़ता है जिसके कारण विभवान्तर प्लेट के मध्य घट जाता है।

प्रश्न 5.
एक समान्तर प्लेट संधारित्र एक स्रोत (बैटरी) से V विभवान्तर तक आवेशित किया गया है, जबकि प्लेटों के मध्य वायु है। संधारित्र को बैटरी से अलग किये बिना वायु के स्थान पर ∈_r परावैद्युतॉक का परावैद्युत माध्यम भर दिया गया है। कारण सहित बताइये कि निम्नलिखित में क्या परिवर्तन होगा ?
(i) विभवान्तर
(ii) प्लेटों के मध्य विद्युत क्षेत्र
(iii) धारिता
(iv) आवेश
(v) ऊर्जा ?
उत्तर:
जब बैटरी जुड़ी रहती है तो
(i) विभवान्तर अपरिवर्तित रहेगा,
(ii) धारिता K गुनी हो जायेगी,
(iii) आवेश q = CV के आधार पर C बढ़ने से बढ़ जायेगा अर्थात् K गुना हो जायेगा,
(iv) विद्युत् क्षेत्र E = [latex]frac{E_{0}}{K}[/latex] घट जायेगा और
(v) ऊर्जा [latex]frac{1}{2}[/latex] CV²
धारिता C बढ़ने से बढ़ जायेगी अर्थात् K गुनी हो जायेगी। यहाँ K परावैद्युतांक है।

प्रश्न 6.
एक समान्तर प्लेट वायु संधारित्र एक विद्युत संभरण से जुड़ा है तथा Vo विभवान्तर तक आवेशित किया गया है। इसको विद्युत संभरण [Supply] से अलग करके इसके प्लेटों के मध्य परावैद्युत पदार्थ भर दिया जाता है। कारण सहित बताइये कि निम्नलिखित में क्या परिवर्तन होगा ?
(i) आवेश
(ii) विभवान्तर
(iii) धारिता
(iv) विद्युत क्षेत्र
(v) ऊर्जा।
उत्तर:
बैटरी हटा लेने के बाद परावैद्युत गुटका खिसकाने से घटकों पर प्रभाव
(i) धारिता K गुनी हो जायेगी,
(ii) आवेश अपरिवर्तित रहेगा,
(iii) विभवान्तर V = [latex]frac{q}{C}[/latex]घट जायेगा क्योंकि धारिता C का मान बढ़ जायेगा,
(iv) विभवान्तर घटने से विद्युत क्षेत्र E = [latex]frac{V}{d}[/latex]भी कम हो जायेगा तथा
(v) U = [latex]frac{1}{2} frac{q^{2}}{mathrm{C}}[/latex] के आधार पर ऊर्जा भी कम हो जायेगी।

प्रश्न 7.
आवेशित संधारित्र में संचित ऊर्जा का सूत्र व्युत्पन्न कीजिये।
उत्तर:
संधात्रि में संवित ऊर्जा(Energy Stored in Capacitor)
किसी चालक को आवेशित करने में जो कार्य किया जाता है, वही आवेशित चालक की ऊर्जा कहलाती है।” जब किसी चालक को आवेश दिया जाता है तो प्रारम्भ में चालक को आवेश का पहला भाग देने में कोई कार्य नहीं करना पड़ता है क्योंकि उस आवेश का कोई विरोध नहीं होता है। इसके बाद जैसे-जैसे आवेश के शेष भाग दिये जाते हैं, तो चालक पर पहले से ही मौजूद आवेश दिये जाने वाले आवेशों का विरोध करते हैं, अत: बाद में दिये जाने वाले सभी आवेशों को देने में इसी प्रतिकर्षण के विरुद्ध कार्य (work done against repulsion) करना पड़ता है। स्पष्ट है कि चालक को आवेश देने में कार्य करना पड़ता है और किसी चालक को आवेश देने में किये गये सम्पूर्ण कार्य को ही आवेशित चालक की ऊर्जा कहते हैं।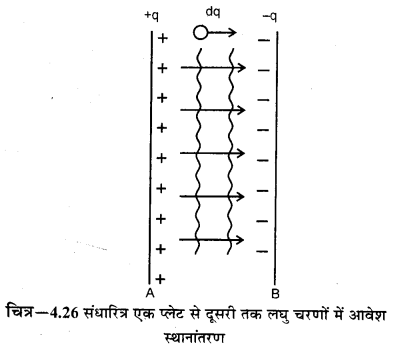

स्थानांतरण | संधारित्र को आवेशित करने में किया गया कार्य ही आवेशित संधारित्र की ऊर्जा कहलाता है। यदि आवेशित संधारित्र की एक प्लेट के आवेश को दूसरी प्लेट तक ले जाया जाये तो संधारित्र अनाविष्ट (uncharged) हो जायेगा। इस क्रिया में जितनी ऊर्जा प्राप्त होगी, वही आवेशित संधारित्र की ऊर्जा होगी।
माना कि संधारित्र का प्रारम्भिक विभवान्तर V है और अनाविष्ट होने पर इसका अन्तिम विभवान्तर शून्य होगा। उक्त क्रिया में संधारित्र का औसत विभवान्तर
[latex]=frac{0+mathrm{V}}{2}=frac{mathrm{V}}{2}[/latex]
यदि संधारित्र पर आवेश q हो तो इस आवेश को एक प्लेट से दूसरी प्लेट तक ले जाने में किया गया कार्य अर्थात् संधारित्र की ऊर्जा
∴ U = W = आवेश × औसत विभवान्तर
= q × [latex]frac{V}{2}[/latex]
U = [latex]frac{1}{2}[/latex] qv
∴ q = CV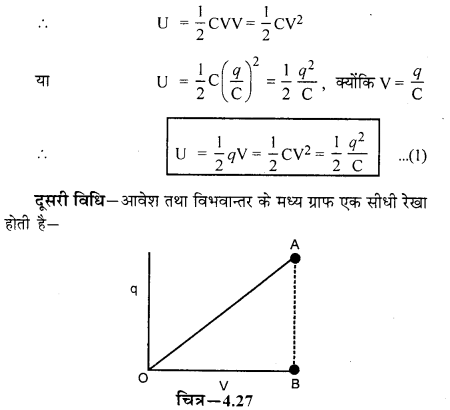

प्रश्न 8.
C धारिता के तीन संधारित्र एक बार श्रेणीक्रम में वे दूसरी बार समान्तर क्रम में जोड़े जाते हैं। इन स्थितियों में तुल्य धारिता का अनुपात क्या होगा ?
उत्तर:
(i) समान्तर क्रम में
C_p = C₁ + C₂ + C₃
= 3C ………….. (i)
(ii) श्रेणीक्रम में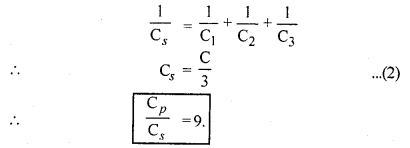

प्रश्न 9.
समान धारिता के n संधारित्रों को श्रेणीक्रम में संयोजित करने पर तुल्य धारिता C_s तथा समान्तर क्रम में संयोजित करने पर तुल्य धारिता Cp है। [latex]frac{C_{p}}{C_{s}}[/latex] का मान ज्ञात कीजिये।
उत्तर:
(i) समान्तर क्रम में
C_p = C₁ + C₂ + C₃
= 3C ………….. (i)
(ii) श्रेणीक्रम में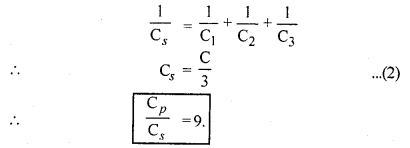

[latex]frac{C_{p}}{C_{s}}[/latex] = n²

प्रश्न 10.
विद्युत धारिता की परिभाषा लिखिये तथा इसका S.I. मात्रक लिखिये।
उत्तर:
चालक की धारिता (Capacitance of Conductor)
धारिता शब्द का अर्थ है ‘धारण करने की क्षमता’, अत: किसी चालक की विद्युत धारिता का अर्थ उसके द्वारा विद्युत आवेश धारण करने की क्षमता (ability to hold electric charge) से है। एक निश्चित सीमा के बाद यदि हम किसी बर्तन में कोई द्रव भरते हैं तो वह फैलने लगता है। इसी प्रकार जब एक निश्चित सीमा के बाद किसी चालक को आवेश दिया जाता है तो उसका विसर्जन (discharge) वातावरण में होने लगता है।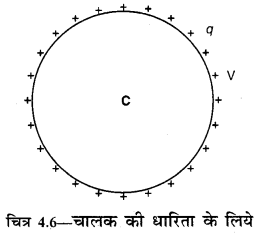

जिस प्रकार किसी बर्तन में डाला गया द्रव उसके गुरुत्वीय तल को बढ़ाता है, ठीक उसी प्रकार किसी चालक को दिया गया आवेश उसके विद्युत तल अर्थात् विद्युत विभव को बढ़ाता है। किसी चालक को जितना अधिक आवेश दिया जाता है, उसका विभव भी उतना ही अधिक बढ़ता है अर्थात् “किसी चालक पर उपस्थित आवेश उसके विभव के अनुक्रमानुपाती होता है।”
∴ q ∝ V
या q = CV …………….. (1)
जहाँ C एक नियतांक है, जिसे चालक की विद्युत धारिता कहते
इस प्रकार चालक की विद्युत धारिता एक नियतांक होती है। इसका मान चालक की आकृति, क्षेत्रफल, चारों ओर के माध्यम तथा पास में रखे अन्य चालकों की उपस्थिति पर निर्भर करता है।
∴ C = [latex]frac{q}{V}[/latex] …………. (2)

प्रश्न 11.
एक गोलीय चालक पर आवेश की मात्रा तीन गुनी करने पर उसकी धारिता पर क्या प्रभाव पड़ेगा ? कारण दीजिये।
उत्तर:
गोलीय चालक की धारिता (C) = 4πε₀R
अत: आवेश का कोई प्रभाव नहीं पड़ेगा।

प्रश्न 12.
2μF धारिता वाले वायु संधारित्र की प्लेटों के मध्य अभ्रक की प्लेट रखने से उसकी धारिता 5μF हो जाती है। अभ्रक का पराविद्युतांक ज्ञात कीजिये।
उत्तर: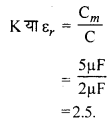

प्रश्न 13.
दो आवेशित चालकों की त्रिज्यायें क्रमशः R₁ व R₂, धारितायें क्रमशः C₁ व C₂ आवेश क्रमशः Q₁ व Q₂ तथा विभव क्रमशः V₁ व V₂ हैं (V₁ > V₂) यदि चालकों को परस्पर एक नगण्य धारिता वाले चालक तार से जोड़ दिया जाता है तब सिद्ध कीजिये कि चालकों के विभव में परिवर्तनों का अनुपात [latex]frac{Delta mathrm{V}_{1}}{Delta mathrm{V}_{2}}=frac{mathrm{C}_{2}}{mathrm{C}_{1}}[/latex] होगा
उत्तर: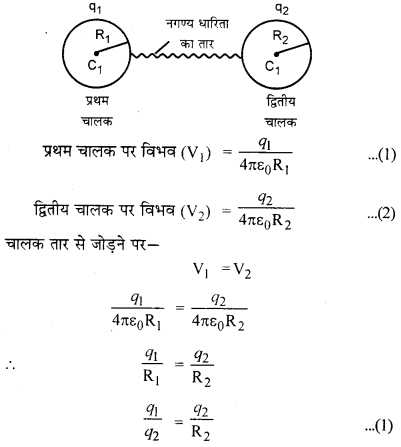

प्रश्न 14.
संधारित्र किसे कहते हैं ? समझाइये।
उत्तर:
संधारित्र (Capacitor)
“वह युक्ति (device) जिसमें चालक के आकार को बिना बदले उसकी धारिता बढ़ायी जा सकती है, संधारित्र कहलाती है।”
संधारित्र में दो परस्पर निकट स्थित चालक प्लेटें होती हैं, जिनमें से एक प्लेट पर धनावेश तथा दूसरी प्लेट पर उतना ही ऋणावेश होता है। इसके लिए दोनों प्लेटों को बैटरी के क्रमशः धन एवं ऋण टर्मिनलों से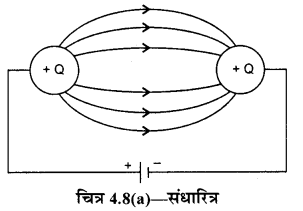

जोड़ा जाता है (चित्र 4.8(a)) अब यदि बैटरी को हटा लिया जाए तो भी चालकों पर आवेश संग्रहित रहता है। अतः संधारित्र को आवेश संचय की युक्ति भी कहा जाता है।

प्रश्न 15.
तीन संधारित्र जिनकी धारितायें क्रमशः C₁ C₂ व C₃ हैं, श्रेणीक्रम में जुड़े हैं। तुल्य धारिता का सूत्र व्युत्पन्न कीजिये।
उत्तर:
श्रेणीक्रम (Series Combination)
उद्देश्य- धारदा को क रने के लिए २ध की श्रेणीक्रम में जोड़ा जाता है।
इसमें एक संधारित्र की दूसरी प्लेट दूसरे संधारित्र की पहली प्लेट से, दूसरे की दूसरी प्लेट तीसरे की पहली प्लेट से तथा इसी प्रकार शेष सभी को जोड़ दिया जाता है (चित्र 4.16) । संयोजन की पहली प्लेट को आवेश दिया जाता है और अंतिम प्लेट को पृथ्वी से सम्बन्धित कर दिया जाता है।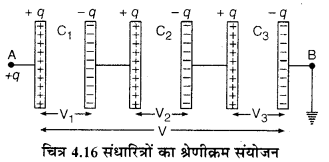

यदि पहले संधारित्र की पहली प्लेट को +q वेश दिया जाये तो प्रेरण द्वारा सभी संधारित्रों की सभी प्लेटों पर एक समान आवेश q होगा, चाहे संधारित्र की धारिता कुछ भी हो। धारिताओं के मान अलग-अलग होने के कारण सभी संधारित्रों की प्लेटों के विभवान्तर अलग-अलग होंगे। यदि पूरे संयोजन का विभवान्तर V हो तो

प्रश्न 16.
तीन संधारित्र जिनकी धारितायें क्रमशः C₁, C₂ व C₃ हैं, समान्तर क्रम में जुड़े हैं। तुल्य धारिता का सूत्र व्युत्पन्न कीजिये।
उत्तर:
पाश्र्व क्रम या समान्तर क्रम संयोजन (Parallel Combination of Capacitors)
उद्देश्य- धारिता को बढ़ाने के लिए संधारित्रों को पाश्र्व क्रम या । समान्तर क्रम में संयोजित किया जाता है।
इस संयोजन में सभी संधारित्रों की पहली प्लेटें एक संधि A व दूसरी प्लेटें दूसरी संधि B के मध्य जोड़ दी जाती हैं। पहली संधि A को + q आवेश दिया जाता है और संधि B को पृथ्वी से सम्बन्धित कर दिया जाता।
है। चूँकि सभी संधारित्र संधियों A व B के मध्य जुड़े होते हैं अत: सबका विभवान्तर (V) समान होता है। संधि A को दिया गया आवेश + q धारिताओं के अनुसार तीनों संधारित्रों में बँट जाता है।
q = q₁ + q₂ + q₃ ………… (i)
चूँकि सभी संधारित्रों का विभवान्तर समान (V) है। अत:
q₁ = C₁V, q₂ = C₂V, q₃ = C₃V
यदि संयोजन की तुल्य धारिता C हो तो
q = CV
समी. (1) में आवेशों के मान रखने पर,
CV = C₁V + C₂V + C₃V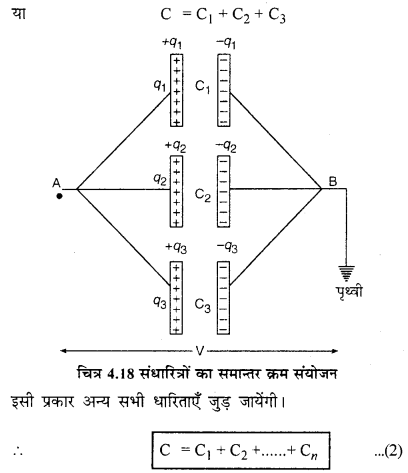

RBSE Class 12 Physics Chapter 4 निबन्धात्मक प्रश्न

प्रश्न 1.
समान्तर प्लेट संधारित्र का सिद्धान्त समझाते हुए इसकी धारिता का व्यंजक स्थापित कीजिये।
उत्तर:
संधारित्र का सिद्धान्त (Principle of Capacitor)
किसी चालक को 4 आवेश देने पर यदि उसका विभव V हो जाता है, तो उसकी धारिता
C = [latex]frac{q}{V}[/latex]
स्पष्ट है कि यदि किसी प्रकार आवेश q के लिए विभव का मान V से कम हो जाये, तो चालक की धारिता C बढ़ जायेगी। इसी विचार से संधारित्र की खोज हुई। संधारित्र का सिद्धान्त (principle) निम्नलिखित तीन पदों में समझा जा सकता है| (i) माना किसी चालक A को q आवेश देने पर उसका विभव V हो जाता है, तो उसकी धारिता
C = [latex]frac{q}{V}[/latex] ……………… (1)
(ii) अब यदि चालक A के पास इसी प्रकार का दूसरा अनावेशित चालक B लाया जाये, तो प्रेरण (induction) द्वारा उसका आवेशन (charging) चित्र 4.8 (c) की भाँति होगा।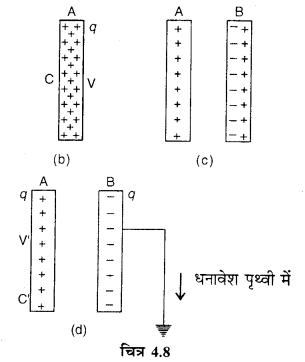

(iii) अब यदि चालक B को पृथ्वी से सम्बन्धित कर दिया जाये, तो उसका समस्त धनावेश पृथ्वी में चला जायेगा। इस नवीन स्थिति में यदि चालक A का विभव V’ हो, तो A की धारिता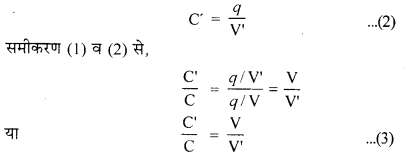

परन्तु V’ = चालक A के आवेश के कारण उत्पन्न विभव
+ चालक B के आवेश के कारण उत्पन्न विभव
या। V’ = V – V”
इसी समीकरण से स्पष्ट है कि
V > V’
∴ समी. (3) से, C’ > C
अर्थात् “जब एक आवेशित चालक के पास दूसरा अनावेशित एवं पृथ्वी से सम्बन्धित चालक लाया जाता है तो पहले चालक की धारिता बढ़ जाती है।” यही संधारित्र का सिद्धान्त है।
इस प्रकार उक्त सिद्धान्त से स्पष्ट है कि संधारित्र में दो पृथक्कृत धात्वीय प्लेटें (separated metallic plates) होती हैं जिसमें एक को आवेश दिया जाता है और दूसरी को पृथ्वी से सम्बन्धित कर देते हैं। जब प्लेटों के मध्य किसी परावैद्युत माध्यम की जगह वायु होती है तो उसे वायु संधारित्र कहते हैं।

समान्तर प्लेट संधारित्र (Parllel Plate Capacitor)
इस संधारित्र में धातु की दो आयताकार प्लेटें एक ही आकार की होती हैं जो एक-दूसरे के आमने-सामने चित्र 4.9 के अनुसार परस्पर समान्तर रखी होती हैं। दोनों प्लेटें विद्युतरोधी स्टैण्डों (insulated stands) पर लगी रहती हैं और दोनों के मध्य K परावैद्युतॉक वाला कोई परावैद्युत माध्यम होता है। एक प्लेट को आवेश दिया जाता है और दूसरी को पृथ्वी से सम्बन्धित (earthing) कर देते हैं।
माना प्रत्येक प्लेट का क्षेत्रफल A मीटर है तथा उनके बीच की दूरी d मीटर है। माना कि प्लेट X को हम +q कूलॉम आवेश देते हैं। प्रेरण द्वारा उसके सामने वाली प्लेट Y के भीतरी तल पर -q कूलॉम आवेश तथा बाहरी तल पर + q कूलॉम आवेश उत्पन्न हो जायेगा। चूँकि प्लेट Y पृथ्वी से जुड़ी है, अत: इसके बाहरी तल का +q कूलॉम आवेश पृथ्वी में चला जायेगा। इस प्रकार प्लेटों X व Y पर बराबर तथा विपरीत आवेश होंगे। प्लेट X से चलने वाली सभी विद्युत बल रेखाएँ प्लेट Y पर पहुँचेगी तथा किनारों को छोड़कर बीच में विद्युत क्षेत्र सभी जगह एकसमान (uniform) होगा।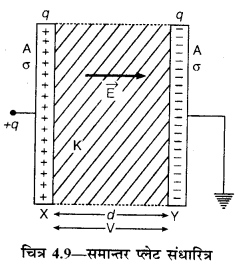

दोनों प्लेटों पर आवेश का पृष्ठ घनत्व (surface charge density)
σ = [latex]frac{q}{A}[/latex]
जहाँ: A प्लेटों का क्षेत्रफल है।
यदि प्लेटों के मध्य दूरी उनके विस्तार (extent) की तुलना में नगण्य (negligible) हो तो उनके मध्य विद्युत क्षेत्र की तीव्रता
E = [latex]frac{sigma}{varepsilon_{0}}[/latex]
जहाँ ε₀ = निर्वात् की विद्युतशीलता यदि प्लेटों के मध्य विभवान्तर V एवं दूरी d हो तो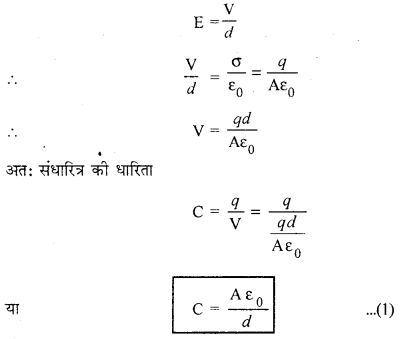

समी. (1) से स्पष्ट है कि समान्तर प्लेट संधारित्र की धारिता निम्न प्रकार बढ़ायी जा सकती है
(i) C ∝ A अर्थात् प्लेटों का क्षेत्रफल बढ़ाकर संधारित्र की धारिता बढ़ायी जा सकती है, लेकिन यह संधारित्र के सिद्धान्त के विरुद्ध है, अतः क्षेत्रफल बढ़ाकर संधारित्र की धारिता नहीं बढ़ायी जाती है।
(ii) C ∝ [latex]frac{1}{d}[/latex] अर्थात् प्लेटों के मध्य दूरी घटाकर संधारित्र की धारिता बढ़ायी जा सकती है।

प्रश्न 2.
आंशिक रूप से भरे परावैद्युत पदार्थ के लिये समान्तर प्लेट संधारित्र की धारिता का व्यंजक व्युत्पन्न कीजिये।
उत्तर:
समान्तर प्लेट संधारित्र की धारिता जबकि परावैद्युत पदार्थ अंशत: भरा हो (Capacitance of Parallel Plate Capacitor Partially Filled with a Dielectric)
उद्देश्य- परावैद्युतांक की सहायता से संधारित्र की धारिता बढ़ाना। माना समान्तर प्लेट संधारित्र की प्लेटों के मध्य दूरी d है और उनके मध्य K परावैद्युतांक (dielectric constant) एवं t मोटाई (thickness) का पुरावैद्युत माध्यम आंशिक (partially) रूप से रखा है। प्लेटों के मध्य वायु वाले क्षेत्र परावैद्युतांक में विद्युत क्षेत्र की तीव्रता [latex]overrightarrow{mathrm{E}}_{0}[/latex] एवं पराविद्युत माध्यम में [latex]overrightarrow{mathrm{E}}[/latex] है। दोनों प्लेटों पर आवेश की पृष्ठ घनत्व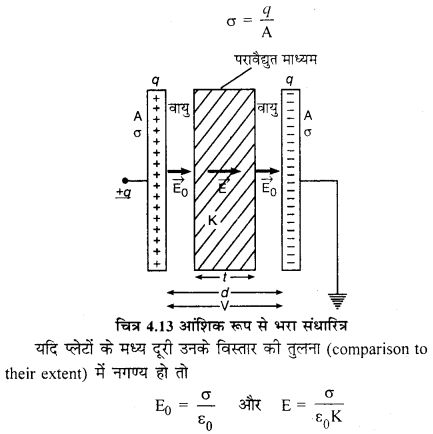

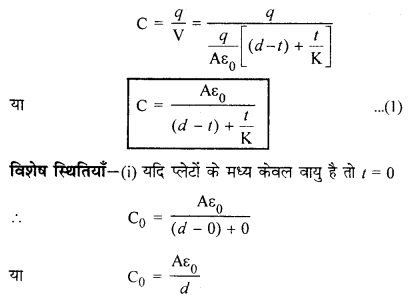
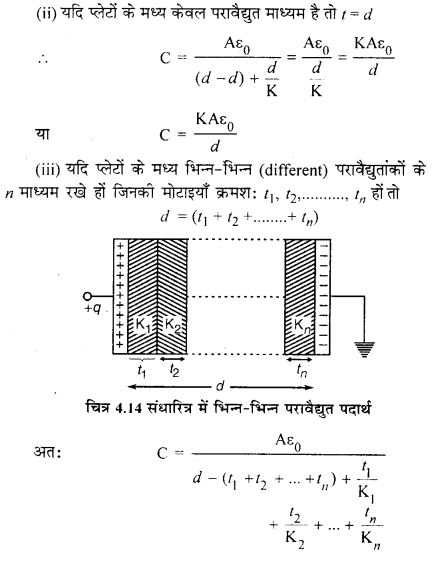
प्रश्न 3.
किसी समान्तर प्लेट संधारित्र की प्लेटों के मध्य विद्युत क्षेत्र के ऊर्जा घनत्व का व्यंजक व्युत्पन्न कीजिये।
उत्तर:
समान्तर प्लेट संधारित्र का ऊर्जा घनत्व (Energy Density of Parallel Plate Capacitor) .
माना समान्तर प्लेट संधारित्र की प्रत्येक प्लेट का क्षेत्रफल A हो तथा उसकी प्लेटों qआवेश दिया जाता है तब उसकी प्लेटों के मध्य विद्युत क्षेत्र (E)
E = [latex]frac{V}{d}[/latex] ⇒ V = Ed

प्रश्न 4.
गोलीय संधारित्र क्या है ? गोलीय संधारित्र की धारिता के लिये व्यंजक व्युत्पन्न कीजिये।
उत्तर:
विलगित गोलीय चालक की धारिता (Capacitance of an Isolated Spherical Conductor)
माना R त्रिज्या का एक गोलाकार चालक K परावैद्युतॉक वाले माध्यम में रखा है। जब इस गोले को +q आवेश दिया जाता है तो यह आवेश गोले के पृष्ठ पर समान रूप से वितरित हो जाता है और फलस्वरूप गोले के पृष्ठ पर विभव V उत्पन्न हो जाता है। गोले का पृष्ठ समविभव पृष्ठ (equi-potential surface) की भाँति व्यवहार करता है। अतः

अर्थात् किसी गोलाकार चालक की धारिता उसकी त्रिज्या के अनुक्रमानुपाती होती है।
यदि गोलीय चालक, किसी परावैद्युत माध्यम में स्थित हो जिसको परावैद्युतॉक ε_r हो तो उसकी धारिता
C_m = [latex]frac{q}{mathrm{V}}[/latex] = 4πε₀ε_rR
C_m = 4πε₀Rε_r
C_m = Cε_r
∴ [latex]frac{C_{m}}{C}[/latex] = ε_r
अत: माध्यम का परावैद्युतॉक माध्यम की विद्युत धारिता एवं वायु (निर्वात्) की विद्युत धारिता के अनुपात के बराबर होती है।

प्रश्न 5.
आवेशित चालकों के संयोजन से आवेशों का पुनर्वितरण समझाइये। आवेश के पुनर्वितरण के पश्चात् आवेशों का अनुपात ज्ञात कीजिये तथा ऊर्जा हानि का सूत्र व्युत्पन्न कीजिये।
उत्तर:
आवेशित चालकों के संयोजन से आवेश का पुनर्वितरण तथा bull sild (Re-distribution of Charges and Loss of Energy by the Combination of Charged Conductors)
माना C₁ व C₂ धारिता के दो चालक A व B हैं। इन्हें q₁ व q₂ आवेश देने पर इनके विभव V₁ व V₂, हो जाते हैं। इनकी ऊर्जाएँ क्रमश: U₁ व U₂ हैं।
जब इन चालकों को किसी पतले संयोजक तार (connecting wire) द्वारा जोड़ देते हैं, तो अधिक विभव वाले चालक से कम विभव वाले चालक पर आवेश का स्थानान्तरण (transfer) तब तक होता रहेगा जब तक दोनों के विभव समान नहीं हो जाते। इसी समान विभव (V) को उभयनिष्ठ विभव (common potential) कहते हैं। दूसरे शब्दों में, चालकों को जोड़ने पर आवेशों का पुनर्वितरण (redistribution ) हो जाता है, यद्यपि आवेश की कुल मात्रा q₁ + q₂ ही रहती है।
प्रारम्भ में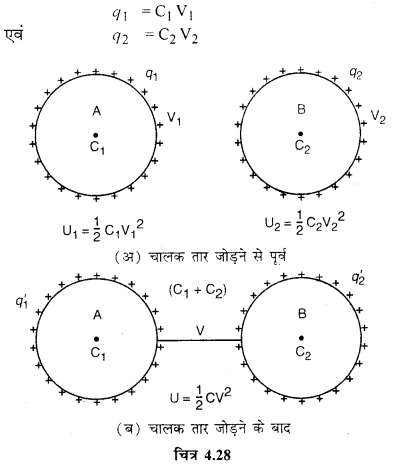

(i) उभयनिष्ठ विभव (Common Potential)- यदि संयोजक तार की धारिता नगण्य (negligible) मान लें, तो पूरे संयोजन की धारिता C = (C₁ + C₂) होगी।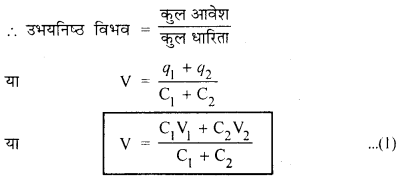

(ii) पुनर्वितरण के बाद (after redistribution) प्रत्येक चालक पर आवेश-चालकों को जोड़ने के बाद आवेशों के पुनर्वितरण के पश्चात् चालक A व B पर आवेश क्रमशः

ऊर्जा हानि (Energy Loss)
आवेशों के पुनर्वितरण प्रक्रिया में आवेश चालक तार से प्रवाहित होता है। इसके परिणामस्वरूप ऊर्जा की कुछ मात्रा ऊष्मा के रूप में परिवर्तित हो जाती है। इस परिवर्तन को ऊष्मा हानि कहते हैं। ऐसा चालक तार के प्रतिरोध के कारण होता है।
(ii) ऊर्जा का ह्रास (Loss of Energy)-चालकों को जोड़ने के पश्चात् चालकों की विद्युत स्थितिज ऊर्जा कुछ कम हो जाती है, अतः ऊर्जा में कमी ΔU = जोड़ने के पहले कुल ऊर्जा – जोड़ने के बाद कुल ऊर्जा
जोड़ने से पहले (before contact),
पहले चालक की विद्युत स्थितिज ऊर्जा
= [latex]frac{1}{2}[/latex] C₁V₁²
दूसरे चालक की विद्युत स्थितिज ऊर्जा
= [latex]frac{1}{2}[/latex] C₂V₂²
∴ जोड़ने से पहले दोनों चालकों की कुल स्थितिज ऊर्जा
U = [latex]frac{1}{2}[/latex] (C₁V₁² + C₂V₂²)
दोनों चालकों को जोड़ने (after contact) पर संयुक्त धारिता (C₁ + C₂) तथा उभयनिष्ठ विभव (common potential) V हो जाता है, अत: दोनों चालकों की कुल स्थितिज ऊर्जा


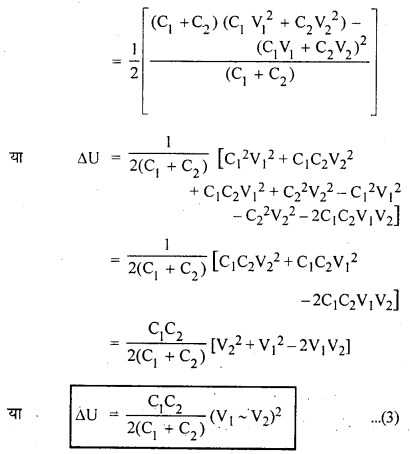
(i) यदि V₁ = V₂ तो (V₁ ~ V₂) = 0
∴ ΔU = 0
अर्थात् जब दोनों चालकों के विभव समान होते हैं, तो ऊर्जा में कोई कमी नहीं होती है क्योंकि इस स्थिति में उन्हें जोड़ने पर आवेशों का पुनर्वितरण नहीं होता है।

(ii) जब V₁ ≠ V₂ तो (V₁ ~ V₂)² = 0
∴ ΔU > 0
अर्थात् ऊर्जा में कमी होगी। ऊर्जा में कमी (loss of energy) का कारण चालकों के मध्य आवेश का पुनर्वितरण (sharing of charges) है। आवेश का प्रवाह संयोजक तार से होकर होता है, अत: संयोजक तोर के प्रतिरोध के विरुद्ध (against the resistance of connecting wire) आवेश के प्रवाहित होने में किया गया कार्य ऊष्मा में बदल जाता है। यही ऊर्जा में कमी का कारण है।

RBSE Class 12 Physics Chapter 4 आंकिक प्रश्न

प्रश्न 1.
एक गोलाकार चालक की धारिता 1pF है। इसकी त्रिज्या ज्ञात कीजिये।
हल:
गोलीय चालक की धारिता (C) = 1pF = 1 × 10^-12F
त्रिज्या (R) = ?
गोलीय चालक की धारिता (C) = 4π ε₀R
R = [latex]frac{mathrm{C}}{4 pi varepsilon_{0}}[/latex] =9 × 10⁹ × 1 × 10^-12
=9 × 10^-3 = 9mm.

प्रश्न 2.
एक समान्तर प्लेट संधारित्र की प्रत्येक प्लेट का क्षेत्रफल 100 cm तथा दोनों प्लेटों के मध्य विद्युत क्षेत्र की तीव्रता 100N/C है। प्रत्येक प्लेट पर आवेश कितना है ?
उत्तर:
दिया है- (A) क्षेत्रफल = 100 cm² = 100 × 10^-4m²
विद्युत क्षेत्र (E) = 100N/C
विद्युत क्षेत्र की तीव्रता (E) = [latex]frac{sigma}{mathrm{A}}=frac{q}{mathrm{A} varepsilon_{0}}[/latex]
∴ q = Aε₀E = 100 × 10^-4 × 8.86 × 10^-12 × 100
= 8.86 × 10^-12 C (प्रत्येक प्लेट पर)

प्रश्न 3.
किसी समान्तर प्लेट संधारित्र को एक निश्चित विभवान्तर पर रखा जाता है। इसके विभवान्तर पद रखा जाता है। इसके विभवान्तर को समान रखते हुए प्लेटों के मध्य 3mm मोटी स्लैब रखी जाती है तो प्लेटों के मध्य दूरी 2.4mm बढ़ानी पड़ती है। स्लैब के परावैद्युतांक की गणना कीजिये।
हल:
समान्तर प्लेट संधारित्र की धारिता (C) = [latex]frac{varepsilon_{0} mathrm{A}}{d}[/latex] …………. (1)
t मोटाई का परावैद्युतांक रखने पर धारिता
C = [latex]frac{varepsilon_{0} mathrm{A}}{d-t+frac{t}{k}}[/latex] ……………. (2)
चूँकि परावैद्युत पट्टिका रखने पर संधारित्र के आवेश में कोई परिवर्तन नहीं होता है। अत: समान्तर प्लेटों के मध्य विभवान्तर को समान बनाये रखने के लिये उसकी धारिता को प्रारम्भिक मान के बराबर ही होना होगा।
यदि अब उसकी प्लेटों के मध्य दूरी d’ हो तो

प्रश्न 4.
दो संधारित्र की धारितायें क्रमशः 2μF तथा 4μF हैं। जब इनको क्रमशः श्रेणीक्रम में तथा समान्तर क्रम में जोड़ा जाता है तो इनकी तुल्य धारिताओं की तुलना कीजिये।
हल:
श्रेणीक्रम में संयोजन से–

प्रश्न 5.
दो आवेशित धातु के गोलों की त्रिज्यायें क्रमश: 0.05m तथा 0.10m हैं। प्रत्येक गोले पर 75μC आवेश है। इन गोलों को पतले तार द्वारा जोड़ने पर (i) उभयनिष्ठ विभव तथा (ii) आवेश प्रवाह की मात्रा ज्ञात करो।
हल:
(i) प्रथम आवेशित धातु के गोले की धार्रिता C₁ = 4πε₀R₁
द्वितीय आवेशित धातु के गोले की धारिता C₂ = 4πε₀R₂

प्रश्न 6.
150 वोल्ट पर आवेशित 2μF धारिता के एक गोलीय चालक का सम्बन्ध 1μF के किसी निरावेशित गोले से कर दिया जाता है। उभयनिष्ठ विभव की गणना करो। प्रत्येक चालक पर आवेश का मान भी ज्ञात करो।
हल:
दिया है-V₁ = 150 वोल्ट, V₂ = 0 (निरावेशित है),
C₁ = 2μF तथा C₂ = 1μF

प्रश्न 7.
125 बूंदों को 200 वोल्ट के विभव तक आवेशित किया जाता है। इन बूंदों को मिलाकर एक बड़ी बूंद बनाते हैं। इससे विभव तथा ऊर्जा में परिवर्तन की गणना कीजिये।
हल:
125 छोटी बूंद का आयतन = एक बड़ी बूंद का आयतन

प्रश्न 8.
चित्र में प्रत्येक संधारित्र की धारिता 1μF है। A व B के मध्य तुल्य धारिता ज्ञात कीजिये।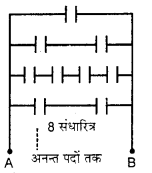

हल:
प्रत्येक भुजा की धारिता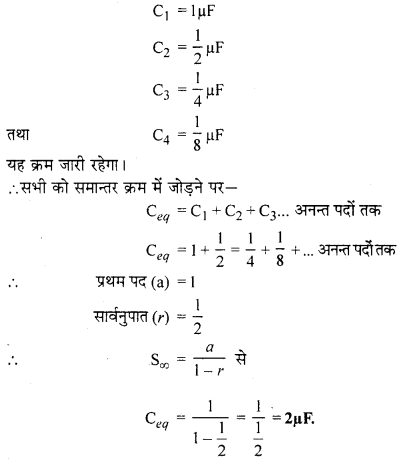

प्रश्न 9.
चित्र में A व B के मध्य तुल्य धारिता 5μF है। संधारित्र C की धारिता ज्ञात करो।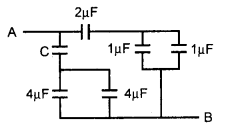

हल:
A तथा B के मध्य तुल्य धारिता C_तल्य = 5μF
1μF तथा 1μF को समान्तर क्रम में जोड़ने पर
C’ = C₁ + C₂ = 1μF + 1μF = 2μF
C’ तथा 2μF को श्रेणीक्रम में जोड़ने पर

प्रश्न 10.
चित्र में दर्शाये गये संधारित्रों की धारिता ज्ञात कीजिये। प्रत्येक प्लेट का क्षेत्रफल A व प्लेटों के मध्य की दूरी d है।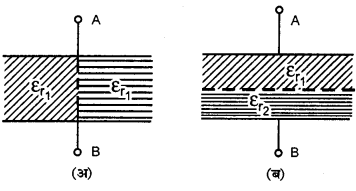

हल:
प्रथम चित्र (अ) में अनुप्रस्थ काट से दो बराबर भागों में बँटा। इसलिए यह दोनों संधारित्र समान्तर क्रम में जुड़ेंगे।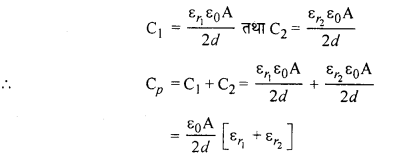

द्वितीय चित्र (ब) में संधारित्र के बीच की दूरी दो बराबर भागों ? बँटी है इसलिये यह दोनों संधारित्र श्रेणीक्रम में संयोजित होंगे।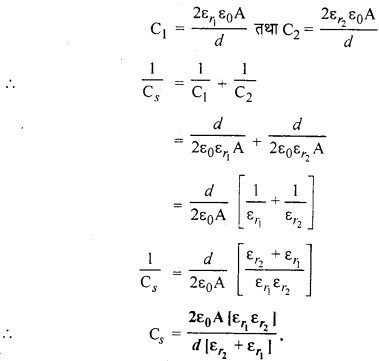

प्रश्न 11.
चित्र में A तथा B के मध्य तुल्य धारिता ज्ञात कीजिये।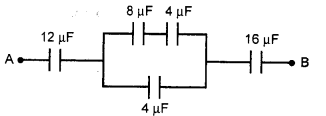

हुल:
8μF तथा 4μF को श्रेणीक्रम में जोड़ने पर

प्रश्न 12.
एक विलगित चालक को दूसरे संकेन्द्रीय गोलीय चालक जिसका बाहरी पृष्ठ पृथ्वी से सम्बन्धित है, से ढक देते हैं। इन गोलीय चालकों की त्रिज्याओं का अनुपात [latex]frac{n}{n-1}[/latex] है। सिद्ध कीजिये कि इस समायोजन से गोलीय चालक की धारिता गुना बढ़ जाती है।
हल:
माना गोलीय चालक की त्रिज्या r₂ है तथा r₁ त्रिज्या से ढका जाता है।
गोलीय चालक की धारिता (C₂) = 4πε₀r₂ …………(1)
द्वितीय स्थिति मेंद्वितीय स्थिति में आधारित गोलीय चालक की संधारित्र की धारिता

प्रश्न 13.
एक समान्तर प्लेट संधारित्र द्वारा संचित ऊर्जा घनत्व 4.43 × 10^-10J/m³ है। संधारित्र की प्लेटों के मध्य विद्युत क्षेत्र की तीव्रता ज्ञात कीजिये। ε₀ = 8.86 × 10^-12F/m.
हल:
ऊर्जा घनत्व (u) = 4.43 × 10^-10 J/m
विद्युत क्षेत्र की तीव्रता E = ?
ऊर्जा घनत्व (u) = [latex]frac{1}{2}[/latex] ε₀E²
4.43 × 10^-10 = [latex]frac{1}{2}[/latex] × 8.86 × 10^-12 × E²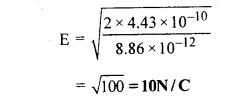

प्रश्न 14.
चित्र में प्रदर्शित निकाय के मध्य की धारिता कितनी होगी यदि प्रत्येक प्लेट का क्षेत्रफल A तथा दो निकटवर्ती प्लेटों के मध्य की दूरी d हो ?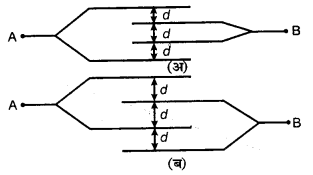

हुल:
महत्वपूर्ण दिशा निर्देश- इस प्रकार के प्रश्नों में एक प्लेट को धनात्मक तथा दूसरी को ऋणात्मक मानने पर, यदि
(1) + प्लेट एक स्थान पर तथा – प्लेट दूसरे स्थान पर प्राप्त हो तो क्रम समानान्तर होगा।
(2) – प्लेट के आगे दूसरी + प्लेट तथा दूसरी -प्लेट के आगे तीसरी (+) है तो श्रेणीक्रम होता है।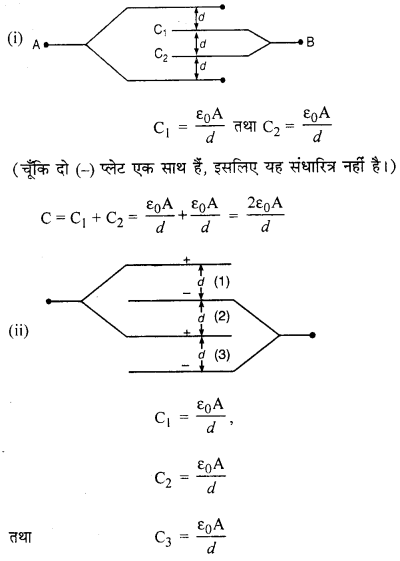

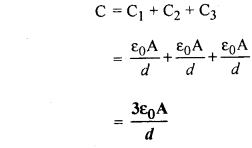
प्रश्न 15.
C धारिता के संधारित्रों को श्रेणीक्रम में संयोजित करने पर तुल्य धारिता C_s तथा समान्तर क्रम में संयोजित करने पर तुल्य धारिता C_p है। सिद्ध कीजिये — C_p – C_s = [latex]frac{left(n^{2}-1right)}{n}[/latex]C
हल:
श्रेणीक्रम में संयोजन से

प्रश्न 16.
एक समान्तर प्लेट संधारित्र में प्रयुक्त प्लेट की त्रिज्या 10 cm है। यदि प्लेटों के मध्य की दूरी 10cm हो तो हवा के लिये संधारित्र की धारिता ज्ञात कीजिये।
हल:
प्लेट की त्रिज्या = 10cm = 10 × 10^-2m
प्लेट की अनुप्रस्थ काट का क्षेत्रफल (A) = πr²
= π × (10 × 10^-2)²
प्लेटों के मध्य दूरी (d) = 10cm = 10 × 10^-2 मी.
समान्तर प्लेट संधारित्र की धारिता (C) = [latex]=frac{varepsilon_{0} mathrm{A}}{d}[/latex]
C = [latex]frac{8.86 times 10^{-12} times 3.14 timesleft(10 times 10^{-2}right)^{2}}{10 times 10^{-10}}[/latex]
= 2.78 × 10^-12F
= 2.78μF.

All Chapter RBSE Solutions For Class 12 Physics

—————————————————————————–

All Subject RBSE Solutions For Class 12

*************************************************

————————————————————

All Chapter RBSE Solutions For Class 12 physics Hindi Medium

All Subject RBSE Solutions For Class 12 Hindi Medium

Remark:

हम उम्मीद रखते है कि यह RBSE Class 12 physics Solutions in Hindi आपकी स्टडी में उपयोगी साबित हुए होंगे | अगर आप लोगो को इससे रिलेटेड कोई भी किसी भी प्रकार का डॉउट हो तो कमेंट बॉक्स में कमेंट करके पूंछ सकते है |

यदि इन solutions से आपको हेल्प मिली हो तो आप इन्हे अपने Classmates & Friends के साथ शेयर कर सकते है और HindiLearning.in को सोशल मीडिया में शेयर कर सकते है, जिससे हमारा मोटिवेशन बढ़ेगा और हम आप लोगो के लिए ऐसे ही और मैटेरियल अपलोड कर पाएंगे |

आपके भविष्य के लिए शुभकामनाएं!!