हेलो स्टूडेंट्स, यहां हमने राजस्थान बोर्ड Class 11 Physics Chapter 9 तरंग गति सॉल्यूशंस को दिया हैं। यह solutions स्टूडेंट के परीक्षा में बहुत सहायक होंगे | Student RBSE solutions for Class 11 Physics Chapter 9 तरंग गति pdf Download करे| RBSE solutions for Class 11 Physics Chapter 9 तरंग गति notes will help you.
Table of Contents
Rajasthan Board RBSE Class 11 Physics Chapter 9 तरंग गति
RBSE Class 11 Physics Chapter 9 पाठ्य पुस्तक के प्रश्न एवं उत्तर
RBSE Class 11 Physics Chapter 9 अतिलघूत्तरात्मक प्रश्न
प्रश्न 1.
तरंग गति में किसका स्थानान्तरण होता है?
उत्तर:
ऊर्जा का स्थानान्तरण होता है।
प्रश्न 2.
एक तनी हुई डोरी की लम्बाई दुगुनी तथा तनाव चार गुना कर दें तो नई आवृत्ति व पूर्व आवृत्ति में क्या सम्बन्ध होगा?
उत्तर:
वे बराबर होंगी।
चूँकि n ∝ (frac{1}{l}) जब T व m स्थिर है।
n ∝ (sqrt{mathrm{T}}) जब l व m स्थिर है।
प्रश्न 3.
कोणीय आवृत्ति, कोणीय तरंग संख्या तथा तरंग वेग में संबंध लिखिए।
उत्तर:
v = (frac{omega}{mathrm{K}}) जहाँ ω → कोणीय आवृत्ति
K → कोणीय तरंग संख्या
v → तरंग वेग
प्रश्न 4.
माध्यम के किसी कण द्वारा एक सैकण्ड में किए गए। कम्पनों की संख्या को क्या कहते हैं?
उत्तर:
आवृत्ति।
प्रश्न 5.
एक कम्पन करने में लिया गया समय क्या कहलाता है?
उत्तर:
आवर्तकाल।
प्रश्न 6.
तरंग वेग समीकरण लिखो।
उत्तर:
v = nλ
प्रश्न 7.
वायु में मानक ताप व दाब पर ध्वनि का वेग कितना होता है? .
उत्तर:
332 मीटर/सेकण्ड
प्रश्न 8.
किसी तरंग का आयाम यदि आधा कर दिया जाये तो उसकी तीव्रता में क्या परिवर्तन आएगा?
उत्तर:
हम जानते हैं I ∝ a2 होता है। इस आधार पर उसकी तीव्रता पूर्व की रह जायेगी।
प्रश्न 9.
किस माध्यम से परावर्तित होने पर परावर्तित तरंग की कला परिवर्तित हो जाती है?
उत्तर:
सघन माध्यम से।
प्रश्न 10.
400 व 402 आवृत्ति के स्वरित्र एक साथ कम्पित कराने पर विस्पन्द की आवृत्ति क्या होगी?
उत्तर:
विस्पन्द की आवृत्ति दोनों स्वरित्रों की आवृत्ति के अन्तर के बराबर होती है।
अतः विस्पन्द की आवृत्ति = n1 – n2
= 402 – 400 = 2
अतः 2 विस्पन्द प्रति सेकण्ड
प्रश्न 11.
समान लम्बाई के खुले व बन्द आर्गन पाइप की मूल आवृत्तियों का अनुपात क्या होगा?
उत्तर:
2 : 1
प्रश्न 12.
खुले या बंद आर्गन पाइप में से किसमें केवल विषम संनादी ही उत्पन्न हो सकती है?
उत्तर:
बन्द में
प्रश्न 13.
माध्य स्थिति से अधिकतम विस्थापन को क्या कहते हैं ?
उत्तर:
आयाम
प्रश्न 14.
क्या अप्रगामी तरंगों के माध्यम से ऊर्जा का स्थानान्तरण होता है?
उत्तर:
नहीं
प्रश्न 15.
अनुनादित वायु स्तम्भ में कौनसी तरंगें उत्पन्न होती हैं?
उत्तर:
अनुदैर्घ्य अप्रगामी तरंगें।
प्रश्न 16.
एक प्रस्पन्द व उसके क्रमिक निस्पन्द के मध्य कितनी दूरी होती है?
उत्तर:
2
प्रश्न 17.
ध्वनि के वेग पर ताप का क्या प्रभाव पड़ता है?
उत्तर:
ताप के साथ वेग बढ़ता है।
प्रश्न 18.
तीक्ष्ण व मोटी ध्वनि में से किसका तारत्व अधिक होता है?
उत्तर:
तीक्ष्ण ध्वनि का।
प्रश्न 19.
क्या पराश्रव्यी वेग से चलने वाले हवाई जहाज की सीटी की ध्वनि में डाप्लर प्रभाव प्रेक्षित होगा?
उत्तर:
नहीं।
RBSE Class 11 Physics Chapter 9 लघूत्तरात्मक प्रश्न
प्रश्न 1.
प्रत्यास्थ तरंगें किन्हें कहते हैं?
उत्तर:
ये तरंगें एक प्रकार की आवर्ती विक्षोभ (disturbance) हैं। जिन्हें एक स्थान से दूसरे स्थान की ओर संचरण करने के लिए माध्यम की आवश्यकता होती है। इन तरंगों को प्रत्यास्थ तरंगें’ कहते हैं।
उदाहरण— ध्वनि तरंगें, जल तरंगें, तनी हुई डोरी या छड़ में तरंगें इत्यादि।
प्रश्न 2.
तरंग के दक्षतापूर्ण संचरण हेतु माध्यम में कौन-कौन | से गुण होने चाहिये?
उत्तर:
तरंग के संचरण के लिए माध्यम के आवश्यक गुण
- तरंग संचरण के लिए माध्यम में अवस्था परिवर्तन का विरोध करने वाला अर्थात् जड़त्व का गुण होना चाहिए।
- माध्य में बल लगाते ही विस्थापित होने तथा बल को हटाने पर प्रारम्भिक अवस्था में आ जाने का अर्थात् प्रत्यास्थता का गुण होना चाहिए।
- सतत तरंग संचरण के लिए माध्यम का प्रतिरोध कम से कम होना चाहिए। .
प्रश्न 3.
तरंग संचरण नियतांक को परिभाषित कीजिये।
उत्तर:
तरंग संचरण नियतांक (Wave Propagation Constant)- यदि तरंग में कम्पित किन्हीं दो बिन्दुओं के बीच की दूरी λ हो तो उनमें कलान्तर 2π होता है। एकांक दूरी पर स्थित कम्पनशील कणों के मध्य कलान्तर को ‘तरंग संचरण नियतांक’ कहते
अर्थात् तरंग संचरण नियतांक K = (frac{2 pi}{lambda})
प्रश्न 4.
अनुप्रस्थ एवं अनुदैर्ध्य तरंगों में क्या अन्तर है? लिखिये।
उत्तर:
अनुप्रस्थ तरंगें (Transverse Waves)- इन तरंगों में माध्यम के कण तरंग संचरण की दिशा में लम्बवत कम्पन करते हैं। अनुप्रस्थ तरंग में ऊपर की ओर अधिकतम विस्थापन की स्थिति को श्रृंग (Crest) तथा नीचे की ओर अधिकतम विस्थापन की स्थिति को गर्त (Trough) कहते हैं।
उदाहरणार्थ, तनी हुई डोरी में उत्पन्न तरंगें, जल के पृष्ठ पर उत्पन्न तरंगें, इत्यादि।
अनुदैर्ध्य तरंगें (Longitudinal Waves)- इन तरंगों में माध्यम के कण तरंग संचरण की दिशा में कम्पन करते हैं तथा संचरण संपीडन (Compression) तथा विरलन (Rarefaction) के रूप में होता है, जिससे तरंग माध्यम में आगे बढ़ती है। संपीडन के स्थान पर माध्यम का घनत्व तथा दाब अधिक व विरलन पर कम हो जाता है।
उदाहरणार्थ, वायु में ध्वनि तरंगें, छड़ों में रगड़ के कारण उत्पन्न तरंगें, इत्यादि।
- अनुप्रस्थ तरंगें केवल उन्हीं माध्यमों में संचरित होती हैं, जिनमें दृढ़ता की गुण विद्यमान हो। स्पष्टतः अनुप्रस्थ तरंगें केवल ठोस एवं द्रवों में गति करती हैं जबकि तरलों में यह संचरण नहीं हो सकती।
- अनुदैर्ध्य तरंगों को आयतन प्रत्यास्थता गुणांक की आवश्यकता होती है। अतः अनुदैर्ध्य तरंगों का संचरण सभी प्रत्यास्थ माध्यमों में कराया जा सकता है। अतः ये तरंगें सभी माध्यमों ठोस, द्रव तथा गैस में सम्भव होती हैं। उदाहरण के तौर पर स्टील की छड़, इसमें अनुप्रस्थ एवं अनुदैर्घ्य दोनों प्रकार की तरंगें संचरित हो सकती हैं जबकि वायु में केवल अनुदैर्थ्य यांत्रिक तरंगों का ही संचरण सम्भव होता है।
प्रश्न 5.
तरंगों के परावर्तन की विवेचना कीजिये
उत्तर-:
तरंगों को परावर्तन (Reflection of Waves)— किसी माध्यम में गतिमान तरंग हेतु यदि माध्यम एक समान है तो तरंग उसी प्रकार गति करती रहेगी परन्तु यदि माध्यम में परिवर्तन होता है तो यह तरंग की गति को भी प्रभावित करता है। जहाँ माध्यम में परिवर्तन होता है, तो दोनों माध्यमों की पृथक्कारी सतह से तरंग का कुछ भाग तो आगे बढ़ जाता है जिसे पारगमित तरंग कहा जाता है, परन्तु कुछ भाग पृथक्कारी सतह से टकराकर पुनः उसी माध्यम में कुछ परिवर्तनों के साथ लौट आता है। इसे ही तरंगों का परावर्तन कहते हैं।
अनुप्रस्थ तरंगों का परावर्तन (Reflection of Transverse Wave)- अनुप्रस्थ तरंगों का परावर्तन को समझने के लिए हम तनी हुई डोरी में, जिसका एक सिरा चित्रानुसार किसी दृढ़ आधार से बंधा हुआ है, चित्रानुसार परावर्तित स्पंद का विस्थापन आपतित स्पंद के विपरीत दिशा में होता है अर्थात् श्रृंग गर्त के रूप में एवं गर्त श्रृंग के रूप में परावर्तित होता है लेकिन इसकी आकृति में कोई अन्तर नहीं होता है।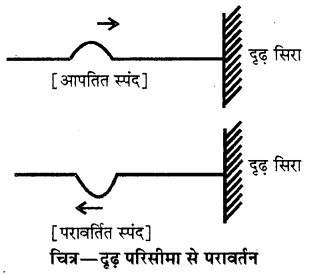
यदि परावर्तन स्वतंत्र सिरे से होता है अर्थात् परिसीमा बिन्दु दृढ़ नहीं है तथा गति के लिए पूर्ण स्वतंत्र है जैसा चित्र में दिखाया गया है, तब श्रृंग शृंग के रूप में तथा गर्त गर्त के रूप में परावर्तित होता है।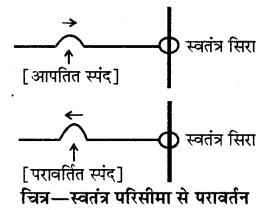
यदि दो विभिन्न मोटाई की डोरियाँ परस्पर जुड़ी हों तब पतली डोरी में तरंग का वेग मोटी डोरी की अपेक्षा अधिक होता है, जो कि तरंग वेग समीकरण v = (sqrt{frac{T}{m}}) के अनुरूप है।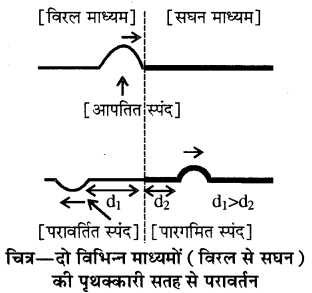
यदि आपतित स्पंद मोटी डोरी से चित्रानुसार पतली डोरी की ओर गतिशील है तो परावर्तित तथा पारगमित स्पंद में विस्थापन की दिशा अपरिवर्तित रहती है।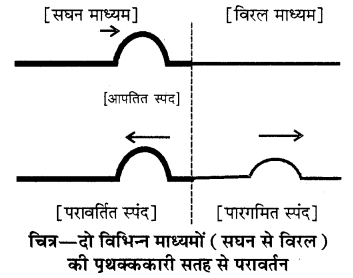
अनुदैर्ध्य तरंगों का परावर्तन (Reflection of Longitudinal Waves)—
- जब सघन माध्यम से अनुदैर्ध्य तरंगें परावर्तित होती हैं। तो सम्पीडन सम्पीडन के रूप में तथा विरलन विरलन के रूप में परावर्तित होते हैं, लेकिन उनकी कला विपरीत हो जाती है।”
- “जब विरल माध्यम से अनुदैर्ध्य तरंगें परावर्तित होती हैं। तो उनकी कला नहीं बदलती है, लेकिन सम्पीडन विरलन के रूप में तथा विरलन सम्पीडन के रूप में परावर्तित होता है।”
उपरोक्त अध्ययन से हम यह निष्कर्ष पर पहुँचते हैं
- एक तरंग विक्षोभ (स्पंद) सघन माध्यम की अपेक्षा विरल माध्यम में अधिक वेग से गति करता है।
- यदि तरंग विरल से सघन माध्यम की ओर गतिशील है तो परावर्तित तरंग (अर्थात् सघन माध्यम से परावर्तित तरंग) की कला विपरीत (अर्थात् से परिवर्तित) हो जाती है तथा यदि परावर्तन विरल माध्यम से होता है तो कला परिवर्तित नहीं होती है।
- दूसरे माध्यम में अपवर्तित तरंग की कला सदैव अपरिवर्तित रहती है।
प्रश्न 6.
प्रगामी एवं अप्रगामी तरंगों की परिभाषा बताइये एवं उनमें अन्तर लिखो।
उत्तर:
1. प्रगामी तरंग (Progressive Wave)- यदि किसी तरग गात माध्यम में तरंग संचरित होने पर माध्यम के कण सरल आवर्त गति से कम्पन करें तो इस तरंग को सरल आवर्त प्रगामी तरंगें कहते हैं।
2. अप्रगामी. तरंगें (Stationary Waves)- जब समान आयाम तथा समान आवृत्ति की दो प्रगामी ध्वनि तरंगें किसी माध्यम में एक-दूसरे की विपरीत दिशा में समान चाल से एक ही रेखा पर चल रही हों तो उनके अध्यारोपण से जो परिणामी तरंग चित्राम बनता है, उसे अप्रगामी तरंग चित्राम कहते हैं।

प्रश्न 7.
तरंगों के अध्यारोपण से आप क्या समझते हैं? स्पष्ट कीजिये।
उत्तर:
जब दो या दो से अधिक तरंगें एक साथ किसी माध्यम में संचरण करती हैं तो किसी क्षण माध्यम के प्रत्येक कण का विस्थापन दोनों तरंगों के पृथक्-पृथक् विस्थापनों के सदिश योग के बराबर होता है। इस सिद्धान्त को ‘अध्यारोपण का सिद्धान्त’ कहते हैं।
यदि किसी क्षण दोनों तरंगों द्वारा विस्थापन y1 व y2 हों तो तरंगों के अध्यारोपण से, परिणामी विस्थापन ।
y = y1 + y2
अध्यारोपण के फलस्वरूप प्राप्त परिणामी तरंग की आवृत्ति तथा आयाम निम्न बातों पर निर्भर करता है-(i) तरंगों की आवृत्ति (ii) तरंगों का आयाम (iii) तरंगों के मध्य कलांतर (iv) तरंगों के संचरण की दिशा
दो ध्वनि तरंगों के अध्यारोपण से विभिन्न परिस्थितियों में निम्न प्रभाव उत्पन्न हो सकते हैं
(1) व्यतिकरण (Interference)- जब दो एक समान तरंगें जिनकी आवृत्ति बराबर है और एक ही दिशा में एक सरल रेखा पर संचरित होती हुई अध्यारोपित होती हैं तो ‘व्यतिकरण’ का प्रभाव उत्पन्न करती हैं।
(2) विस्पन्द (Beats)—दो असमान (लगभग बराबर) आवृत्ति की तरंगें जो एक ही दिशा में चल रही हैं, विस्पन्द (Beats) उत्पन्न करती हैं।
(3) अप्रगामी तरंगें (Stationary waves)- दो समान तरंगें जिनकी आवृत्ति बराबर है, परन्तु माध्यम में एक सीध में विपरीत दिशा में चलती हैं, अध्यारोपण से अप्रगामी तरंगें (Stationary waves) उत्पन्न करती हैं।
(4) लिसाजू की आकृतियाँ (Lissajou’s Figures)- जब किसी कण पर एक ही समय दो परस्पर लम्बवत् सरल आवर्त गतियाँ अध्यारोपित होती हैं तो कण का परिणामी विस्थापन सदिश एक वक्रीय पथ पर चलता है, जिसकी आकृति गतियों के पृथक्-पृथक् आयाम, आवर्तकाल तथा उनमें कलान्तर पर निर्भर करती है। इन आकृतियों को लिसाजू की आकृतियाँ (Lissajou’s figures) कहते हैं।
प्रश्न 8.
गैस में तरंग वेग व्यंजक हेतु लाप्लास संशोधन की विवेचना कीजिये।
उत्तर:
लाप्लास संशोधन-लाप्लास के अनुसार जब वायु में ध्वनि तरंगें चलती हैं तो वायु का संपीडन एवं विरलन होता है। संपीडन के स्थानों पर वायु के कण पास-पास होने के कारण गर्म हो जाते हैं व विरलन की स्थिति में कणों के दूर होने के कारण उनका ताप कम हो। जाता है तथा संपीडन एवं विरलन एक के बाद दूसरा प्रक्रम इतनी तेजी से होते हैं कि ऊष्मा को माध्यम से बाहर जाकर ताप नियत रखना संभव नहीं होता। अतः इस प्रक्रम के दौरान ताप नियत नहीं रहता है। अतः यह क्रिया समतापीय के स्थान पर रुद्धोष्म होती है।
अतः रुद्धोष्म परिवर्तन हेतु गैस समीकरण से।
PVγ = (P + ΔP) (V+ ΔV)γ
= P(1+ (frac{Delta P}{P}))Vγ (1 + (frac{Delta V}{V}))γ
या PVγ = PVγ = (1 + (frac{Delta P}{P}))(1 + (frac{Delta V}{V}))γ
γ का मान एक परमाणुक गैस हेतु 1.67 तथा द्विपरमाणुिक गैस हेतु 1.41 होता है। अतः सूत्र (2) का प्रयोग करने पर मानक ताप व दाब पर वायु में ध्वनि का वेग
Vवायु = (sqrt{frac{1.41 times 1.01 times 10^{5}}{1.29}})
= 332 m/s जो कि प्रायोगिक मान के समरूप है।
उपरोक्त अध्ययन से हम देखते हैं कि ठोस माध्यम में ध्वनि का वेग अधिकतम व गैस माध्यम में न्यूनतम होता है।
प्रश्न 9.
तनी हुई डोरी में अनुप्रस्थ कम्पन के नियम लिखिए।
उत्तर:
तनी हुई डोरी के अनुप्रस्थ कम्पनों के नियम (Laws of Transverse Vibrations of a Stretched String)- तनी हुई डोरी के अनुप्रस्थ कम्पनों की मूल आवृत्ति
n = (frac{1}{2 l} sqrt{frac{mathrm{T}}{mathrm{m}}})
जहाँ l = डोरी की कम्पित लम्बाई
T= डोरी पर आरोपित तनाव तथा
m = डोरी की एकांक लम्बाई का द्रव्यमान
इस सूत्र के आधार पर डोरी की अनुप्रस्थ कम्पनों के निम्नलिखित नियम प्राप्त होते हैं
(1) लम्बाई का नियम (Law of Length)- यदि डोरी के तनाव बल T एवं एकांक लम्बाई का द्रव्यमान (m) नियत हो तो कम्पित डोरी की आवृत्ति
n ∝ (frac{1}{l})
या n × 1 = नियतांक
या n1l1 = n2l2 = n3l3 = नियतांक
n और (frac{1}{l}) में ग्राफी खींचने पर एक सरल रेखा प्राप्त होती है। इससे भी लम्बाई के नियम का सत्यापन होता है।
(2) तनाव का नियम (Law of Tension)— यदि डोरी की लम्बाई l व उसके एकांक लम्बाई का द्रव्यमान m नियत हों तो डोरी की आवृत्ति उसके तनाव के वर्गमूल के समानुपाती होती है।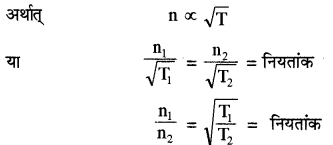
(3) द्रव्यमान का नियम (Law of Mass)- यदि डोरी की लम्बाई l तथा उसमें तनाव T नियत रहें तो डोरी की आवृत्ति उसकी एकांक लम्बाई के द्रव्यमान के वर्गमूल के व्युत्क्रमानुपाती होती है।
अथवा n (sqrt{frac{1}{m}})
अर्थात् n × mt/2 = नियतांक
अथवा (mathrm{n} sqrt{mathrm{m}}) = नियतांक
यदि एक ही तनाव पर समान लम्बाई के m1 व m2 एकांक लम्बाई के द्रव्यमान वाले तारों के कम्पन की संगत आवृत्तियाँ क्रमशः n1 तथा n2 हों, तो इस नियम के अनुसार,
(frac{mathrm{n}_{1}}{mathrm{n}_{2}}=sqrt{frac{mathrm{m}_{2}}{mathrm{m}_{1}}})
चूँकि डोरी की प्रति एकांक लम्बाई का द्रव्यमान
m = πr2d
जहाँ r = डोरी की त्रिज्या तथा d = डोरी के पदार्थ का घनत्व अतः उपर्युक्त द्रव्यमान के नियम के आधार परे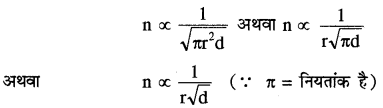
प्रश्न 10.
सोनोमीटर में अप्रगामी तरंगों का निर्माण किस प्रकार होता है? स्पष्ट कीजिये।
उत्तर:
डोरी के अनुप्रस्थ कम्पनों का अध्ययन जिस उपकरण से किया जाता है, उसे सोनोमीटर कहते हैं। यह एक आयताकार खोखला बढ़िया किस्म की मुलायम लकड़ी का बक्सा होता है, जिसमें चित्रानुसार सुराख होते हैं, जिससे बॉक्स में उत्पन्न कम्पन बाहर सुनाई पड़ सके इसे अनुनाद बॉक्स भी कहते हैं। ध्वनि बॉक्स दो ऊध्र्वाधर टाँगों पर टिका होता है तथा इसकी ऊपरी सतह पर एक तार हुक से बँधा होता है। तार का दूसरा सिरा एक घिरनी से लटका हुआ हैंगर से सम्बन्धित होता है, जिस पर भार रखकर तार में वांछनीय तनाव उत्पन्न किया जाता है। बॉक्स की सतह पर दो सेतु (Bridge) एवं किनारे पर एक मीटर पैमाना लगा होता है। सेतुओं का उपयोग कम्पित तार की लम्बाई बदलने में किया जाता है। जब तार को कर्षित (Plucked) किया जाता है, तब वह अनुप्रस्थ कम्पन करते हुए अप्रगामी तरंगें बनाता है। तार के कम्पन से सोनोमीटर का खोखला बॉक्स भी अनुनादित होकर उन्हीं कम्पनों को देता है और इस प्रकार ध्वनि की प्रबलता बढ़ती है। बिना बॉक्स के ध्वनि की प्रबलता बहुत कम होगी।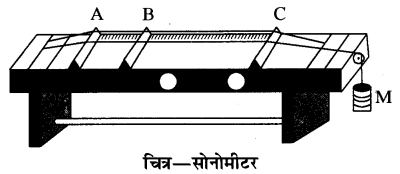
प्रश्न 11.
अवमंदित कम्पन एवं पोषित कम्पन की विवेचना कीजिये।
उत्तर:
आदर्श मुक्त कम्पन में वस्तु का आयाम नियत रहता है। लेकिन वास्तव में जब वस्तु मुक्त कम्पन करती है तो जिस माध्यम में वह कम्पन कर रही है, उसके कारण वह कुछ घर्षण बल अनुभव करती है। फलस्वरूप उसकी ऊर्जा का कुछ भाग ऊष्मा के रूप में नष्ट हो जाता है। अतः वस्तु का आयाम समय के साथ कम होता जाता है, इस प्रकार के कम्पन जिनका आयाम समय के साथ कम होता जाता है, ‘अवमन्दित कम्पन’ कहलाते हैं।
यदि किसी प्रकार से हम कम्पन करने वाली वस्तु को जितनी उसकी ऊर्जा में हानि होती है, उतनी ही उसे देते रहें तो वह वस्तु नियत आयाम से कम्पन करती रहती है। इस प्रकार के कम्पन को ‘पोषित कम्पन’ कहते हैं।
प्रश्न 12.
यदि किसी तरंग की तरंगदैर्घ्य 2500 हो तो तरंग संख्या क्या होगी?
उत्तर:
तरंगदैर्घ्य का व्युत्क्रम तरंग संख्या कहलाती है। यह एकांक दूरी में तरंगों की संख्या को व्यक्त करती है।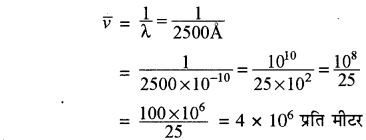
प्रश्न 13.
प्रस्पन्द एवं निस्पन्दों की विवेचना कीजिये।
उत्तर:
- माध्यम के कुछ कण (A1, A2, A3, A4, A5) सदैव अपनी माध्य स्थिति के दोनों ओर अधिकतम आयाम से कम्पन्न करते रहते हैं, इन्हें प्रस्पन्द’ (Antinode) कहा जाता है। प्रस्पन्दों पर कणों का वेग (left(frac{d y}{d t}right)) अधिकतम होता है तथा दाब या घनत्व परिवर्तन शून्य होता है। (left(because frac{d y}{d x}=0right))
- क्रमागत प्रस्पन्दों के बीच के कण (N1, N2, N3, N4) सदैव स्थिर रहते हैं। इन्हें ‘निस्पन्द’ (Node) कहते हैं। ये समान दूरियों पर स्थिर रहते हैं। निस्पन्दों पर कणों का वेग (left(frac{d y}{d t}right)) शून्य होता है तथा दाब या घनत्व परिवर्तन अधिकतम होता है।
- एक आवर्तकाल में दो बार माध्यम के सभी कण एक साथ अपनी साम्यावस्था में आते हैं। अर्थात् एक आवर्तकाल में दो बार सभी कणों का विस्थापन शून्य होता है।
- एक निस्पन्द के दोनों ओर के कण विपरीत कला में कम्पन्न करते हैं तथा प्रस्पन्द के दोनों ओर स्थित कण समान कला में होते हैं।
- दो क्रमागत प्रस्पन्दों या दो क्रमागत निस्पन्दों के बीच की दूरी λ/2 होती है तथा एक निस्पन्द व उसके समीपस्थ प्रस्पन्द के बीच की दूरी λ/4 होती है जहाँ λ तरंग की तंरगदैर्घ्य है।
प्रश्न 14.
तरंग की तीव्रता का मान किन-किन पर निर्भर करता है?
उत्तर:
यदि ρ घनत्व के माध्यम में एक सरल आवर्त प्रगामी तरंग v चाल से चल रही है, तो तरंग की तीव्रता
I = 2π2n2a2ρv
जहाँ n तरंग की आवृत्ति तथा a माध्यम के कणों के कम्पन का आयाम है।
माध्यम के घनत्व ρ का मान नियत होता है और तरंग गति के लिए v नियत होने से I ∝ a2 तथा I ∝ n2
अर्थात् तरंग की तीव्रता (I) कम्पन के आयाम के वर्ग (a2) के तथा कम्पन की आवृत्ति के वर्ग (n2) के अनुक्रमानुपाती होती है।
प्रश्न 15.
विस्पन्द विधि द्वारा किसी स्वरित्र की आवृत्ति किस प्रकार ज्ञात करते हैं? .
उत्तर:
यदि हमें किसी स्वरित्र की आवृत्ति n1 ज्ञात हो तो हम किसी दूसरे स्वरित्र की आवृत्ति जो लगभग n1 के बराबर है, विस्पन्दों की सहायता से ज्ञात कर सकते हैं। इसके लिए दोनों स्वरित्रों को साथसाथ बजाते हैं। माना कि एक सेकण्ड में ∆n विस्पंद सुनाई पड़ते हैं तो दूसरे स्वरित्र की आवृत्ति n1 + ∆n अथवा n1 – ∆n होगी। अब इस स्वरित्र की भुजा पर थोड़ा-सा मोम लगाकर इसकी आवृत्ति कुछ कम कर देते हैं फिर दोनों स्वरित्रों को पुनः साथ-साथ बजाकर विस्पन्द सुनते हैं। यदि विस्पन्दों की संख्या पहले से घटती है तो इसका अर्थ यह हुआ कि दूसरे स्वरित्र की आवृत्ति कम किये जाने पर पहले स्वरित्र की आवृत्ति के और पास आ गई है।
यह तभी सम्भव है जबकि दूसरे स्वरित्र की आवृत्ति पहले स्वरित्र की अपेक्षा अधिक हो। अतः दूसरे स्वरित्र की आवृत्ति n1 + ∆n है। इसके विपरीत यदि मोम लगाने पर विस्पन्दों की संख्या पहले से अधिक हो जाती है तो दूसरे स्वरित्र की आवृत्ति n1 – ∆n होगी।
प्रश्न 16.
डाप्लर प्रभाव की सीमाएँ क्या हैं? लिखिए।
उत्तर:
डॉप्लर प्रभाव को प्रेक्षित करने के लिए आवश्यक है कि ध्वनि स्रोत, श्रोता एवं माध्यम प्रत्येक का वेग ध्वनि के वेग से कम हो। यदि इनका वेग ध्वनि के वेग से अधिक है तो तरंगाग्र विकृत हो जाता है तथा प्रघाती तरंगें (Shock Waves) उत्पन्न हो जाती हैं। डॉप्लर प्रभाव प्रेक्षित नहीं होता है। उदाहरण जैसे-जैट विमान।
प्रश्न 17.
ध्वनि तरंगों में डाप्लर प्रभाव किन-किन पर निर्भर करता है?
उत्तर:
डॉप्लर प्रभाव एक तरंग परिघटना है। यह केवल ध्वनि तरंग पर ही लागू नहीं होता, बल्कि सभी विद्युत चुम्बकीय तरंगों पर लागू होता है।
प्रश्न 18.
स्रोत किस वेग से श्रोता की ओर चले कि आभासी आवृत्ति दुगुनी हो जाये?
उत्तर:
हम जानते हैं
= 
प्रश्न 19.
डॉप्लर प्रभाव के उपयोग से पनडुब्बी का वेग किस प्रकार ज्ञात करते हैं?
उत्तर:
पनडुब्बी को वेग ज्ञात करना-डॉप्लर प्रभाव का। उपयोग पनडुब्बी (Submarine) का वेग ज्ञात करने में किया जाता है। पनडुब्बी का वेग ज्ञात करने के लिए समुद्र तट से ध्वनि तरंगें समुद्र में भेजी जाती हैं, वे पनडुब्बी से परावर्तित होकर पुनः समुद्र तट पर स्थित सोनार स्टेशन पर ग्रहण की जाती हैं। परावर्तित तरंग के तरंगदैर्ध्य में परिवर्तन होता है। जब पनडुब्बी का वेग पानी में ध्वनि के वेग से बहुत कम हो तो तरंगदैर्ध्य में परिवर्तन का सूत्र होगा
∆λ = λ’ – λ = ± (left(frac{2 v_{0}}{v}right) lambda)
जहाँ पनडुब्बी का वेग v0 है।
जब पनडुब्बी सोनार स्टेशन (Sonar Station) से दूर जा रही है। तो समीकरण में धनात्मक चिन्ह होगा अर्थात् परावर्तित तरंगों की तरंगदैर्घ्य बढ़ती है। जब पनडुब्बी सोनार स्टेशन के पास आ रही है तो (उपरोक्त समीकरण) में ऋणात्मक चिन्ह होगा अर्थात् परावर्तित तरंगों की तरंगदैर्घ्य घटती है। इस सूत्र का उपयोग करके पनडुब्बी का वेग (v0) ज्ञात किया जा सकता है।
RBSE Class 11 Physics Chapter 9 निबन्धात्मक प्रश्न
प्रश्न 1.
तरंग गति से आप क्या समझते हैं? स्पष्ट कीजिए। प्रगामी तरंग समीकरण हेतु व्यंजक एवं तरंग का एक विमीय अवकल समीकरण प्राप्त कीजिए।
उत्तर:
हम अपने वातावरण में बहुत-सी घटनाओं को देखते हैं जैसे कि तालाब अथवा झील की सतह पर लहरें, तालाब के शान्त जल में पत्थर का टुकड़ा फेंकने पर विक्षोभ (Disturbance) उत्पन्न होना। कुछ ही समय में इस हलचल का प्रभाव हमें पानी की सतह के अन्य भागों में देखने को मिलता है। यदि इस स्थिति में पानी की सतह पर एक कॉर्क रख दें तो हम देखते हैं कि कॉर्क तो अपने स्थान पर ही ऊपर-नीचे कम्पन करता है जबकि हलचल आगे की ओर बढ़ती रहती है।
इसी प्रकार, रस्सी के एक सिरे को बराबर कम्पन कराने पर रस्सी में स्पन्द एक के पीछे एक तेजी से अग्रसित होते हैं। रस्सी में बढ़ते हुए स्पन्दों की इस श्रृंखला को तरंग कहते हैं।”
किसी माध्यम में एक स्थान से दूसरे स्थान तक ऊर्जा संरचरण की। मुख्यतः दो विधियाँ हैं। पहली विधि में पदार्थ के कण स्वयं ऊर्जा लेकर एक स्थान से दूसरे स्थान तक जाते हैं। अर्थात् इस विधि में पदार्थ का वास्तव में स्थानान्तरण होता है। द्वितीय विधि में ऊर्जा का संचरण माध्यम के एक कण से दूसरे कण, दूसरे कण से तीसरे, तीसरे कण से चौथे, इत्यादि, में होता रहता है जब तक कि ऊर्जा अंतिम कण तक नहीं पहुँच जाती इस विधि में वास्तव में पदार्थ का स्थानान्तरण नहीं होता है। ऊर्जा संचरण की इस विधि को तरंग गति कहते हैं।
तरंग गति में माध्यम के कण अपना स्थान नहीं छोड़ते तथा साम्यावस्था के इर्द-गिर्द कम्पन करते रहते हैं। माध्यम में ऊर्जा तथा संवेग का स्थानान्तरण होता है व माध्यम के कणों की कला सतत रूप से परिवर्तित होती रहती है।
तरंगों को मुख्यतः तीन प्रकार से वर्गीकृत किया गया है
1. विद्युत चुम्बकीय तरंगें (Electromagnetic Waves)- वे तरंगें जिनमें एक स्थान से दूसरे स्थान तक ऊर्जा के संचरण हेतु माध्यम की आवश्यकता नहीं होती, विद्युत चुम्बकीय तरंगें कहलाती हैं।
प्रकाश किरण, एक्स किरणें, रेडियो तरंगें, ऊष्मीय विकीरण, रेडियो तरंगें, गामा विकीरण आदि विद्युत चुम्बकीय तरंगें हैं।
2. द्रव्य तरंगें (Matter Waves)- जब किसी द्रव्य के कण जैसे इलेक्ट्रॉन, प्रोटॉन, न्यूट्रॉन आदि गति करते हैं तो गतिमान कण से सम्बद्ध तरंगों को द्रव्य तरंगें कहा जाता है। इलेक्ट्रॉन सूक्ष्मदर्शी में इलेक्ट्रॉन से सम्बद्ध द्रव्य तरंगों का उपयोग किया जाता है।
3. यांत्रिक तरंगें (Mechanical Waves)- ये तरंगें एक प्रकार की आवर्ती विक्षोभ (disturbance) हैं जिन्हें एक स्थान से दूसरे स्थान की ओर संचरण करने के लिए माध्यम की आवश्यकता होती है। इन तरंगों को प्रत्यास्थ तरंगें’ भी कहते हैं।
तरंग गति में निम्न गुणधर्म प्रेक्षित होते हैं
- यह माध्यम के कणों के सतत रूप से आवर्ती गति के कारण उत्पन्न किया गया विक्षोभ है।
- केवल तरंग (ऊर्जा) आगे बढ़ती है तथा वही तरंग संचरण की दिशा होती है जबकि माध्यम के कण अपनी माध्य स्थिति के आसपास कम्पन करते रहते हैं।
- माध्यम के कणों की कला में लगातार परिवर्तन होता रहता है। आगे का कण अपने पिछले कण से कुछ समय पश्चात् कम्पन्न करना प्रारम्भ करता है।
- जिस वेग से विक्षोभ आगे बढ़ता है, उसे तरंग का वेग कहा जाता है। तरंग का वेग माध्यम के कणों के वेग से भिन्न होता है। तरंग का वेग नियत होता है जबकि कणों का वेग भिन्न-भिन्न स्थितियों में भिन्न-भिन्न होता है। इन तरंगों का माध्य स्थिति पर वेग अधिकतम तथा विस्थापन की स्थिति में वेग शून्य होता है तरंग एक स्थान से दूसरे स्थान तक पहुँचने में निश्चित समय लेती है।
- तरंग अन्य माध्यम की सीमा पर पहुँचकर परावर्तित या अपवर्तित हो सकती है।
- इसमें व्यतिकरण और विवर्तन का गुणधर्म होता है।
माध्यम के द्वारा तरंग के दक्षतापूर्ण संचरण हेतु आवश्यक गुण
- तरंग संचरण के लिए माध्यम में अवस्था परिवर्तन का विरोध करने वाला अर्थात् जड़त्व का गुण होना चाहिए ताकि वह ऊर्जा को एकत्रित कर सके अन्यथा ऊर्जा का क्षय हो जायेगा।
- मध्य में बल लगाते ही विस्थापित होने तथा बल को हटाने पर प्रारम्भिक अवस्था में आ जाने का अर्थात् प्रत्यास्थता का गुण होना चाहिए।
- सतत् तरंग संचरण के लिए माध्यम का प्रतिरोध कम-सेकम होना चाहिए।
उपर्युक्त गुण यांत्रिक तरंग गति हेतु हैं। यदि तरंग विद्युत चुम्बकीय है तो वे बिना माध्यम के निर्वात में भी गति करती है और उसमें तरंग गति के समस्त गुण विद्यमान रहते हैं। पूर्व में हमने तरंगों का वर्गीकरण उनके भौतिक गुणों के आधार पर किया है, जिसमें विभिन्न प्रकार की तरंगों में भेद इस आधार पर किया जाता है कि माध्यम के कणों की गति तरंग गति से किस प्रकार से सम्बन्धित (Related) है। इस आधार पर तरंग दो प्रकार की होती है-(a) अनुदैर्ध्य तरंगें (b) अनुप्रस्थ तरंगें।
प्रगामी तरंग समीकरण
(Progressive wave Equation)
यदि किसी माध्यम में तरंग संचरित होने पर माध्यम के कण सरल आवर्त गति से कम्पन करें तो इस तरंग को सरल आवर्त प्रगामी तरंग कहते हैं। माध्यम के कण समान व अलग-अलग कलाओं में कम्पन करते रहते हैं।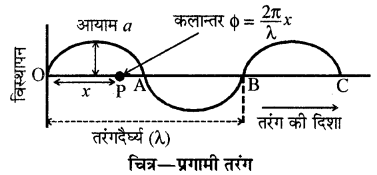
माना कोई तरंग बिन्दु O से दायीं ओर चित्रानुसार v वेग से गतिशील है।
बिन्दु O के दायीं ओर के कण कुछ समय बाद विक्षोभित होते हैं अतः इस कारण उनकी गति पश्चगामी होती है। मूल बिन्दु O से x दूरी पर स्थित बिन्दु P पर स्थित किसी कण के लिए विस्थापन समीकरण
y = a sin (ωt – ϕ) ……………….. (1)
यहां ϕ, O व P पर स्थित कणों के मध्य कलान्तर है। चूंकि बिन्दु P, O से x दूरी पर है तथा λ दूरी पर स्थित कणों में कलान्तर 2π होता है
अतः x दूरी पर स्थित कणों में कलान्तर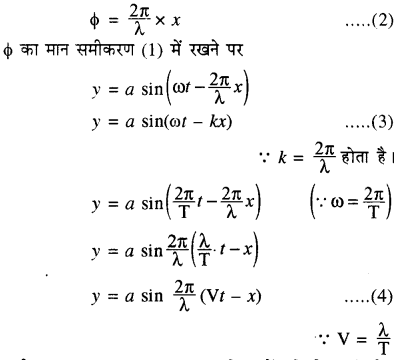
समीकरण (3) व (4) धनात्मक x दिशा में गतिशील तरंग हेतु प्रगामी तरंग समीकरण को व्यक्त करते हैं।
इसी प्रकार ऋणात्मक x दिशा में संचरित तरंग हेतु तरंग समीकरण y = a sin (ωt + kx) से दिया जाएगा।
पुनः समीकरण (3) से
y = a sin (ωt – kx)
उपरोक्त समीकरण का समय के सापेक्ष अवकलन करने पर
y = (frac{d y}{d t}) = a cos (ωt – kx) …………..(5)
यह कण के वेग हेतु व्यंजक है। अतः स्पष्ट है कि कण का वेग तरंग वेग से अलग है। कण का वेग समय (t) तथा कण की स्थिति (x) पर निर्भर करता है जबकि तरंग वेग नियत होता है। समीकरण (5) से कण के वेग का अधिकतम संभव मान ωa है।
पुनः समीकरण (5) का समय के सापेक्ष अवकलन करने पर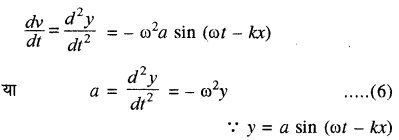
यहाँ a = (frac{d^{2} y}{d t^{2}}) कण का त्वरण है। समीकरण (6) यह दर्शाता है कि कण का त्वरण विस्थापन के समानुपाती तथा विपरीत दिशा में है। यह सरल आवर्त गति की आवश्यक शर्त है। समीकरण (3) का स्थिति x के सापेक्ष दो बार अवकलन करने पर
समीकरण (9) तरंग का एक विमीय अवकल समीकरण कहलाता है।
प्रश्न 2.
तरल में तरंग के वेग हेतु व्यंजक प्राप्त कीजिए।
उत्तर:
अनुदैर्ध्य तरंगों का संचरण तथा उनका वेग (Propagation of longitudinal waves and their velocity)
अनुदैर्ध्य तरंगों के संचरण एवं उनका वेग ज्ञात करने के लिए हम एक पिस्टन लगी नली जिसमें सम्पीय तरल भरा है, जिसे समान्तर रेखाओं द्वारा समान द्रव की कई परतों में विभाजित किया गया है, जहाँ रेखायें पास-पास हैं, वहाँ तरल का दाब तथा घनत्व अधिक है, जहाँ पर रेखायें दूर-दूर हैं वहाँ दाब तथा घनत्व कम है। यहाँ पर हमें तरल को सतत माध्यम मानकर चलेंगे और इस बात की उपेक्षा भी करेंगे कि वास्तव में यह अणुओं से मिलकर बना है, जो भिन्न-भिन्न दिशाओं में भिन्न-भिन्न वेगों से गतिशील है।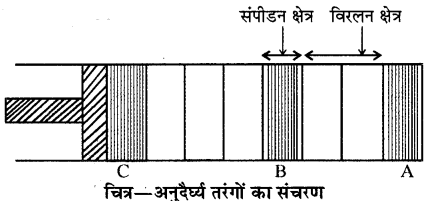
यदि हम पिस्टन को नली के अन्दर की ओर धक्का दें तो इसके सम्पर्क से तरल को संपीडन होगा तथा इसका दाब एवं घनत्व बढ़ेगा। संपीडित तरल की यह परत आगे की ओर गति करेगी और आगे वाली परत में संपीडन उत्पन्न करेगी। यदि हम पुनः पिस्टन को बाहर की ओर खींचें तो इसके सम्पर्क से तरल फैलेगा तथा उसका दाब एवं घनत्व कम होगा अर्थात् यहाँ पर विरलन होगा। इस प्रकार यदि पिस्टन को सतत रूप से अन्दर-बाहर करते रहें तो विक्षोभ नली में संपीडन एवं विरलन के रूप में आगे की ओर बढ़ता जायेगा अतः यह अनुदैर्ध्य तरंग की तरह व्यवहार करता है।
माना पिस्टन को अन्दर की ओर धक्का देकर एक विक्षोभ उत्पन्न किया जाता है जो कि संपीडन के रूप में है तथा दायीं ओर v वेग से गतिशील है। सरलता के लिए सम्पीडन क्षेत्र के अन्दर तरल का दाब व घनत्व एक समान है। अब यदि प्रेक्षक भी संपीडन की दिशा में समान वेग से गतिशील माना जाये तो तरल माध्यम v वेग संपीडन की विपरीत दिशा में गति करता हुआ प्रतीत होगा एवं प्रेक्षक के आगे संपीडन स्थिर होगा। इस स्थिति में जब तरल v वेग से संपीडन क्षेत्र की ओर गति करता हुआ जब संपीडन क्षेत्र से टकराता है तब इसके आगे के किनारे पर पीछे के किनारे से दाब कुछ अधिक होगा। माना इन दोनों किनारों का दाबान्तर ΔP है। इस कारण इस क्षेत्र B में तरल माध्यम संपीडित होगा तथा इस क्षेत्र में इसका वेग कुछ कम माना (V – ΔV) होगा तथा यह अल्पांश इस संपीडन क्षेत्र से बाहर निकलेगा तो पुनः अपने प्रारंभिक आयतन को प्राप्त कर लेगा तथा दाबान्तर ΔP के कारण पीछे की ओर दाब अधिक होने के कारण त्वरित होगा। इस कारण इसका वेग पुनः v हो जायेगा। इस प्रकार यह अल्पांश C स्थिति में पहुँच जाएगा।
जब तरल अल्पांश संपीडन क्षेत्र में प्रवेश करता है तो उस पर दायीं ओर कार्यरत परिणामी बल
(F) = दाब (P) × क्षेत्रफल (A)
= (P + ΔP) A – PA
= PΔ + ΔPA – PA = ΔPA
जहाँ A नली का अनुप्रस्थ काट का क्षेत्रफल है। सम्पीडन क्षेत्र के बाहर इस अल्पांश की लम्बाई vΔt है।
अतः अल्पांश का आयतन = vΔt × A
अल्पांश का द्रव्यमान = आयतन x घनत्व
= vΔt × A × ρ
जहाँ ρ सरल का संपीडन क्षेत्र से बाहर घनत्व है। जब यह अल्पांश संपीडन क्षेत्र में प्रवेश करता है तो उसके द्वारा अनुभव किया गया त्वरण
a = (-frac{Delta v}{Delta t})
(चूँकि वेग कम होता है अतः त्वरण ऋणात्मक है।) अब न्यूटन की गति के द्वितीय नियम से
बल (F) = द्रव्यमान (m) × त्वरण (a)
अत: तरल माध्यम में अनुदैर्ध्य तरंग का वेग v = (sqrt{frac{mathbf{E}}{rho}}) होगा। इससे स्पष्ट है कि तरंग का वेग माध्यम के गुणों, प्रत्यास्थता गुणांक तथा घनत्व पर निर्भर करता है।
प्रश्न 3.
एक समान तनी हुई डोरी में अनुप्रस्थ तरंगों के वेग हेतु सूत्र व्युत्पन्न कीजिए।
उत्तर:
तनी हुई डोरी में अनुप्रस्थ तरंगों का वेग (Velocity of transverse waves in a streched string)
हम जानते हैं कि तनी हुई डोरी में विक्षोभ से अनुप्रस्थ तरंगें उत्पन्न होती हैं। अतः अनुप्रस्थ तरंगों का वेग ज्ञात करने के लिए, माना एक डोरी, जिसकी इकाई लम्बाई का द्रव्यमान m है, तथा तनाव T है, इसमें विक्षोभ बायीं ओर से दायीं ओर V वेग से गतिशील है। और हम यह भी कल्पना कर सकते हैं कि प्रेक्षक विक्षोभ की दिशा में समान वेग। V से गतिशील है तो प्रेक्षक को स्पंद स्थिर प्रतीत होगा तथा डोरी विपरीत दिशा में गति करती हुई प्रतीत होगी।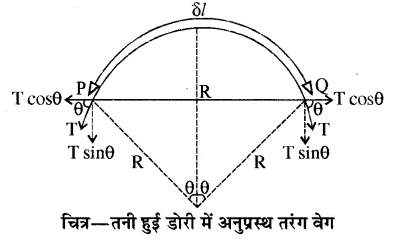
अब हम अल्पांश लम्बाई δl पर विचार करते हैं तो विक्षोभ के कारण यदि डोरी में अल्प विस्थापन हो तो इस अल्पांश δl को चित्रानुसार R क्रिया के वृत्त के चाप का एक हिस्सा माना जा सकता है। तथा इस अल्पांश का द्रव्यमान mδl होगा।
चित्रानुसार केन्द्र की ओर तनावों का घटक 2T sin θ आवश्यक अभिकेन्द्रीय बल प्रदान करेगा अतः
यह अनुप्रस्थ तरंग के वेग का समीकरण है। यह समीकरण स्पष्ट करता है कि डोरी में तरंग का वेग उसमें तनाव तथा एकांक लम्बाई के द्रव्यमान पर निर्भर करता है तथा तरंग के आयाम तथा उसकी तरंगदैर्घ्य पर निर्भर नहीं करता।
प्रश्न 4.
सिद्ध करो कि तार में अनुदैर्ध्य तरंगों व अनुप्रस्थ तरंगों के वेग का अनुपात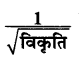
होता है।
हल:
तने हुए तार में अनुप्रस्थ तरंग की चाल निम्नांकित सूत्र से व्यक्त की जाती है
v = (sqrt{left(frac{mathrm{T}}{m}right)}) …………. (1)
जहाँ T तार में तनाव है तथा m तार की एकांक लम्बाई का द्रव्यमान है।
यदि तार पर M द्रव्यमान लटकाकर उसमें T तनाव आरोपित किया जाये तो
T= Mg
तब m = πr2d
जहाँ पर r तार की त्रिज्या तथा d घनत्व है।
अनुदैर्ध्य तरंगों की चाल- जब ठोस एक तार के रूप में है तब उसमें अनुदैर्ध्य तरंग की चाल
v = (sqrt{frac{y}{d}}) ………… (4)
जहाँ पर y = तार के पदार्थ का यंग प्रत्यास्थता गुणांक
d = तार के पदार्थ का घनत्व
अनुदैर्ध्य तरंगों व अनुप्रस्थ तरंगों के वेग का अनुपात लेने पर
समीकरण (5) में मान रखने पर
अनुदैर्ध्य तरंगों व अनुप्रस्थ तरंगों के वेगों का अनुपात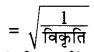
प्रश्न 5.
तरंग के आयाम एवं तीव्रता में संबंध हेतु व्यंजक व्युत्पन्न कीजिए।
उत्तर:
तरंग के आयाम एवं तीव्रता में सम्बन्ध
(Relation between Amplitude and Intensity of a Wave)
जब किसी माध्यम में प्रगामी तरंग संचरित होती है तो वह तरंग माध्यम के उत्तरोत्तर कणों को ऊर्जा प्रदान करती है जिससे ये कण क्रमिक रूप से आवर्ती कम्पन करना प्रारंभ करते हैं। यह ऊर्जा तरंग स्रोत से प्राप्त होती है। चूंकि माध्यम के कण इस दौरान सरल आवर्ती गति करते हैं अतः कणों की सम्पूर्ण ऊर्जा उनकी गतिज ऊर्जा तथा स्थितिज ऊर्जा के योग के बराबर होती है। इसलिए हम माध्यम के एकांक आयतन की ऊर्जा अर्थात् ऊर्जा घनत्व ज्ञात करते हैं।
प्रगामी तरंग के लिए कण की विस्थापन
y = a sin (frac{2 pi}{lambda}) (vt – x) …………..(1)
जहाँ a = कण का आयाम,
λ. = तरंगदैर्घ्य,
t = समय,
x = मूल बिन्दु से कण की दूरी
अतः इस कण का वेग
u = (frac{d y}{d t})
(यहाँ पर u कण का वेग व v तरंग का वेग है)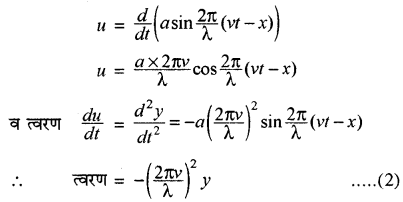
समीकरण (1) को प्रयोग करने पर
अब माना तरंग संचरण की दिशा के लम्बवत् तथा मूल बिन्दु से x दूरी पर dx मोटाई व एकांक परिच्छेद क्षेत्रफल की परतें लेते हैं, तब
इसका द्रव्यमान
m = आयतन × घनत्व
m = 1 × dx × ρ
या m = ρdx …………………. (3)
चूँकि परतें बहुत पतली हैं, अतः इस परत के सभी कणों का वेग ॥ माना जा सकता है। तब कणों की गतिज ऊर्जा
K = (frac{1}{2}) mu2
= (frac{1}{2} times rho d x timesleft(frac{2 pi v a}{lambda}right)^{2} cos ^{2} frac{2 pi}{lambda}(v t-x)) ………….(4)
यदि इस परत को इसकी माध्य स्थिति से सूक्ष्म दूरी dy से विस्थापित करें तो बल के विपरीत किया गया कार्य
dW = – Fdy = – द्रव्यमान × त्वरण × dy
dW = – ρdx × – (left(frac{2 pi v}{lambda}right)^{2}) ydy
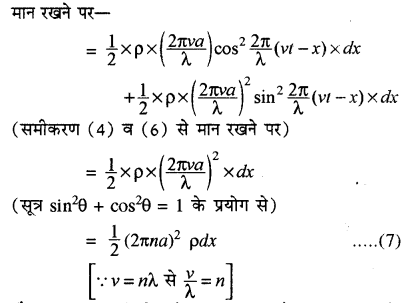
चूँकि परत का परिच्छेद क्षेत्रफल एकांक है अतः माध्यम के एकांक आयतन हेतु सम्पूर्ण ऊर्जा (ऊर्जा घनत्व) परत की एकांक लम्बाई में निहित ऊर्जा के बराबर होगी। अतः समीकरण (7) का x = 0 से 1 तक समकलन करने पर
ऊर्जा घनत्व = (int_{0}^{1} frac{1}{2}(2 pi n a)^{2} times rho d x)
= (frac{1}{2} times(2 pi n a)^{2} times rho times 1)
ऊर्जा घनत्व = 2π2a2a2ρ ……………. (8)
उपरोक्त समीकरण (8) से स्पष्ट है कि ऊर्जा घनत्व दूरी x तथा समय t पर निर्भर नहीं करता है।
तरंग गति की दिशा के लम्बवत् एकांक क्षेत्रफल से प्रति सेकण्ड प्रवाहित ऊर्जा को ऊर्जा फ्लक्स कहते हैं। चूँकि एक सेकण्ड में एकांक क्षेत्रफल से होकर जाने वाली ऊर्जा माध्यम की लम्बाई v अतः आयतन = v × 1 = v
चूंकि तरंग का वेग = v है।
ऊर्जा फ्लक्स = आयतन v में कणों की ऊर्जा
= 2π2a2a2ρv
तथा किसी तरंग की तीव्रता एकांक समय में माध्यम के एकांक क्षेत्रफल पर आपतित ऊर्जा के बराबर होती है अर्थात् माध्यम के एकांक क्षेत्रफल से ऊर्जा के बहने की दर को तरंग की तीव्रता कहते हैं। अतः तरंग की तीव्रता I = 2π2a2a2ρv ……………(9)
इसका मात्रक वाट/मीटर होता है।
समीकरण (9) से स्पष्ट है कि
(i) तरंग की तीव्रता तरंग के आयाम के वर्ग के अनुक्रमानुपाती होती है अर्थात्
I ∝ a2
(ii) तरंग की तीव्रता तरंग की आवृत्ति के वर्ग के अनुक्रमानुपाती होती है अर्थात्
I ∝ n2
(iii) तरंग की तीव्रता माध्यम के घनत्व के अनुक्रमानुपाती होती है अर्थात्
I ∝ ρ
(iv) तरंग की तीव्रता माध्यम में तरंग की चाल के । अनुक्रमानुपाती होती है अर्थात्
I ∝ v
प्रश्न 6.
अप्रगामी तरंग किसे कहते हैं? अप्रगामी तरंग हेतु परिणामी तरंग समीकरण प्राप्त कीजिए।
उत्तर:
जब समान आयाम तथा समान आवृत्ति की दो प्रगामी ध्वनि तरंगें किसी माध्यम में एक-दूसरे की विपरीत दिशा में समान चाल से एक ही रेखा पर चल रही हों तो उनके अध्यारोपण से जो परिणामी तरंग चित्राम बनता है उसे अप्रगामी तरंग चित्राम कहते हैं । परिणामी तरंग विक्षोभ तथा ऊर्जा का किसी भी दिशा में संचरण नहीं होता है। परिणामी तरंग के बनने के लिए माध्यम सीमित होना चाहिए। अप्रगामी तरंगें दो प्रकार की होती हैं–(i) अनुदैर्ध्य अप्रगामी तरंगें (ii) अनुप्रस्थ अप्रगामी तरंगें।
(i) अनुदैर्ध्य अप्रगामी तरंगें- जब दो समान आवृत्ति एवं समान आयाम की अनुदैर्ध्य तरंगें एक ही सरल रेखा पर विपरीत दिशा में गति करती हुई अध्यारोपित होती हैं तो माध्यम में इनके अध्यारोपण से अनुदैर्ध्य अप्रगामी तरंगें बनती हैं।
उदाहरणार्थ, वायु स्तम्भों में बनने वाली अप्रगामी तरंगें।
(ii) अनुप्रस्थ अप्रगामी तरंगें- जब दो समान आवृत्ति एवं समान आयाम की अनुप्रस्थ तरंगें एक ही सरल रेखा पर विपरीत दिशा में गति करती हुई अध्यारोपित होती हैं तो माध्यम में इनके अध्यारोपण से अनुप्रस्थ अप्रगामी तरंगें बनती हैं।
उदाहरणार्थ-स्वरमापी तार वाले वाद्ययंत्र, मेल्डीज प्रयोग, इत्यादि में बनने वाली तरंगें।
अप्रगामी तरंगों के बनने की शर्त
अप्रगामी तरंग बनने के लिए माध्यम असीमित नहीं होना चाहिए बल्कि इसकी एक परिसीमा होनी चाहिए अर्थात् माध्यम बद्ध होना चाहिए क्योंकि इस प्रकार के माध्यम में संचरित कोई प्रगामी तरंग माध्यम की परिसीमा पर परावर्तित होकर अपने ही अनुरूप तथा विपरीत दिशा में संचरित तरंग उत्पन्न करती है। इन आपतित एवं परावर्तित तरंगों के अध्यारोपण के फलस्वरूप ही अप्रगामी तरंग बनती है।
इस प्रकार अप्रगामी तरंगों के बनने के लिए बद्ध माध्यम का होना एक आवश्यक शर्त है।”
निस्पन्द (Nodes) एवं प्रस्पन्द (Anti-nodes)— अप्रगामी तरंग की मुख्य विशेषता यह है कि इसमें माध्यम के कुछ बिन्दुओं पर स्थित कण स्थायी रूप से विरामावस्था में रहते हैं, अर्थात् उनका विस्थापन सदैव शून्य रहता है। इन बिन्दुओं को निस्पन्द (nodes) कहते हैं। इसके विपरीत माध्यम के कुछ अन्य बिन्दुओं पर स्थित कणों का विस्थापन सदैव अन्य बिन्दुओं पर स्थित कणों के विस्थापन की अपेक्षा अधिकतम रहता है। माध्यम के इन बिन्दुओं को प्रस्पन्द (Anti-nodes) कहते हैं। माध्यम में निस्पन्द एवं प्रस्पन्द एकान्तर क्रम से बनते हैं। दो निकटतम निस्पन्दों अथवा दो निकटतम प्रस्पन्दों के बीच की दूरी तरंग की तरंगदैर्ध्य की आधी अर्थात् (left(frac{lambda}{2}right)) होती है, जबकि निकटतम एक निस्पन्द व एक प्रस्पन्द के बीच की दूरी तरंगदैर्घ्य की चौथाई अर्थात् (left(frac{lambda}{4}right)) होती है।
अप्रगामी तरंगों का गणितीय विश्लेषण
(Mathematical Analysis of Stationary Waves)
माना एक प्रगामी तरंग x-अक्ष की धनात्मक दिशा में संचरित हो रही है जिसका आयाम a, आवर्तकाल T तथा तरंगदैर्घ्य λ है। इस तरंग का समीकरण होगा
y1 = a sin (ωt – kx) …………….. (1)
माना कि यह तरंग किसी मुक्त (Free) सिरे से टकराती है और परावर्तित तरंग -अक्ष की ऋण दिशा में अग्रसर होती है तब परावर्तित तरंग का समीकरण निम्न होगा
y2 = a sin (ωt + kx) …………. (2)
परन्तु यदि यही तरंग किसी दृढ़ सिरे से परावर्तित हो तब परावर्तित तरंग का समीकरण निम्न होगा
y2 = -a sin (ωt + kx) ……….. (3)
सघन माध्यम से परावर्तन के कारण तरंग की कला में 7 का परिवर्तन हो जाता है। अतः आयाम a से पूर्व ऋणात्मक चिन्ह होगा।
दोनों परावर्तित तरंगों में से किसी को भी लेकर अप्रगामी तरंग का समीकरण प्राप्त किया जा सकता है। यहाँ पर मुक्त सिरे से परावर्तित प्रगामी तरंग को लेकर अप्रगामी तरंग का समीकरण प्राप्त करेंगे।
अध्यारोपण के सिद्धान्त से परिणामी विस्थापन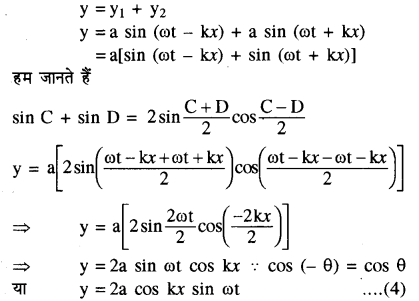
यह अप्रगामी तरंग समीकरण है जिसका आयाम R = 2a cos kx है। स्पष्ट है कि आयाम का मान दूरी x पर निर्भर करता है।
स्थिति-I
तो kx = (left(frac{2 pi}{lambda}right)(2 n+1) frac{lambda}{4}=(2 n+1) frac{pi}{2}) (n = 0, 1, 2, ……………)
∴ cos kx = (cos left(frac{2 pi}{lambda}right) x) का मान शून्य होगा अतः आयाम R का मान शून्य होगा। इन बिन्दुओं पर विस्थापन शून्य हो जाता है। इन्हें निस्पन्द कहते हैं तथा ये एक-दूसरे से (frac{lambda}{2}) की दूरी पर स्थित हैं। उपर्युक्त स्थितियों से स्पष्ट है कि दो क्रमागत निस्पन्द अथवा प्रस्पन्द के बीच की दूरी (frac{lambda}{2}) तथा क्रमागत प्रस्पन्द व निस्पन्द के मध्य दूरी (frac{lambda}{4}) होती है।
इस प्रकार अधिकतम आयाम की स्थितियों को प्रस्पन्द तथा आयाम की स्थितियों को निस्पन्द कहते हैं तथा दो क्रमागत निस्पन्दों के मध्य एक प्रस्पन्द होता है।
y = 2a cos kx sin ωt
= 2acoskxsin(left(frac{2 pi}{mathrm{T}} mathrm{t}right))
यदि किसी विशिष्ट कण के लिए x नियत हो, का विस्थापन भिन्न-भिन्न समयों पर भिन्न-भिन्न होगा। यदि t = 0, (frac{mathrm{T}}{2}), (frac{mathrm{2T}}{2}), (frac{mathrm{3T}}{2}) हो (sin left(frac{2 pi}{mathrm{T}} mathrm{t}right))
मान शून्य होगा। स्पष्ट है कि इन क्षणों पर माध्यम के सभी कणों का विस्थापन शून्य होता है। x का मान चाहे कुछ भी हो यह भी स्पष्ट है कि सभी कण प्रत्येक कम्पन में दो बार अपनी-अपनी साम्यावस्था के साथ-साथ गुजरते हैं।
यदि t = (frac{mathrm{T}}{4}), (frac{mathrm{3T}}{4}) ……… हो तो (sin left(frac{2 pi}{mathrm{T}} mathrm{t}right)) का मान एकान्तर क्रम में +1 तथा -1 होगा अर्थात् इन क्षणों पर माध्यम के सभी कणों का विस्थापन अधिकतम होता है तथा एकान्तर क्रम में धनात्मक व ऋणात्मक होता है। इससे स्पष्ट होता है कि माध्यम के कण प्रत्येक कम्पन में दो बार अधिकतम विस्थापन की स्थिति में होते हैं।
यहाँ E आयतन प्रत्यास्थता गुणांक है।
∴ ΔP =E[-2ak sin(kx) sin(ωt)]
ΔP =-2ak E sin(kx) sin(ωt)
यदि तरंग छड़ सिरे (सघन माध्यम) से परावर्तित होती है, तो
y1 = a sin(ωt – kx)
y2 = – a sin(ωt + kx)
परिणामी विस्थापन
y = y1 + y2
= a sin(ωt – kx) – a sin(ωt + kx)
= a[sin(ωt – kx) – sin(ωt + kx)]
= a[-2sin(kx) cos(ωt)]
y = -2a sin(kx) cos(ωt) ……………… (5)
माध्यम के कणों का वेग
प्रश्न 7.
अनुनाद किसे कहते हैं? अनुनाद नली का चित्र बनाकर वर्णन करते हुए वायु में ध्वनि का वेग ज्ञात करने हेतु व्यंजक प्राप्त कीजिए।
उत्तर:
अनुनाद (Resonance)
जब कम्पन करने वाली किसी वस्तु को उसकी साम्यावस्था से थोड़ा विस्थापित करके छोड़ दिया जाता है तब वह प्रत्यानयन बल के प्रभाव में कम्पन करना प्रारम्भ कर देती है। यदि वस्तु पर प्रत्यानयन बल के अतिरिक्त कोई अन्य बल जैसे घर्षण बल आदि नहीं लग रहा हो तो उसके कम्पनों का आयाम नियत रहता है तथा उसकी यांत्रिक ऊर्जा संरक्षित रहती है। ऐसे कम्पनों को मुक्त कम्पन (Free vibration) कहते हैं। इन कम्पनों की आवृत्ति केवल वस्तु के प्रत्यानयन बल पर निर्भर करती है। कम्पित वस्तु की इस आवृत्ति को प्राकृतिक आवृत्ति या मूल आवृत्ति कहते हैं। वास्तव में, वस्तु जिस माध्यम में कम्पन कर रही है उसके द्वारा कम्पित वस्तु पर कुछ घर्षण बल अवश्य लगता है। इस कारण वस्तु के दोलनों या कम्पनों का आयाम समय के सापेक्ष कम होता जाता है और इसकी यांत्रिक ऊर्जा भी धीरे-धीरे कम होती जाती है। इस प्रकार के कम्पनों को अवमंदित कम्पन कहते हैं।
यदि किसी प्रकार से हम कम्पन करने वाली वस्तु को जितनी उसकी ऊर्जा में हानि होती है, उतनी ही ऊर्जा उसे देते रहें तो वह वस्तु नियत आयाम से कम्पन करती रहती है। इस प्रकार के कम्पन को ‘पोषित कम्पन’ कहते हैं।
एक कम्पन करती हुई वस्तु (चालक) अन्य कम्पन कर सकने वाली वस्तु (जो कि चालित) को कम्पन करने के लिए विवश करती है। यदि उनकी मूल आवृत्तियाँ भिन्न हैं, तब भी यह सम्भव है। इस प्रकार के कम्पन को ‘प्रणोदित कम्पन’ कहते हैं। ऐसे कम्पन जल्दी ही समाप्त हो जाते हैं क्योंकि इस स्थिति में चालित वस्तु अपनी मूल आवृत्ति से कम्पन नहीं करती जबकि वह चालक की आवृत्ति से कम्पन करती है।
जब बाह्य बल या चालक की आवृत्ति चालित वस्तु की मूल आवृत्ति के बराबर हो जाती है तो बाह्य बल से चालित वस्तु को ऊर्जा विनिमय सर्वाधिक होता है तथा प्रणोदित कम्पनों का आयाम बहुत अधिक हो जाता है। इस अवस्था को अनुनाद की अवस्था कहते हैं। अनुनाद की स्थिति में आयाम अवमन्दन बल पर निर्भर करता है। यदि अवमंदन शून्य हो तो अनुनाद की स्थिति में आयाम अनन्त तक बढ़ सकता है।
अनुनाद नली की सहायता से वायु में ध्वनि का वेग ज्ञात करना (Determination of Velocity of Sound in Air with the help of resonance tube)
अनुनाद नली वह उपकरण है जिसकी सहायता से वायु स्तम्भ में कम्पन कराकर अनुनाद की स्थिति उत्पन्न करके वायु में ध्वनि का वेग ज्ञात किया जाता है।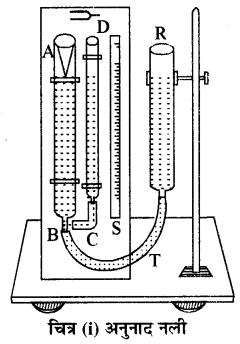
चित्र में दर्शाये अनुसार यह एक धातु या काँच की 1 मीटर लम्बी नली होती है। जिसका व्यास लगभग 5 सेमी. होता है। यह नली एक लकड़ी के ऊर्ध्वाधर स्टैण्ड में कसी होती है। इसके निचले सिरे पर रबर की नली के द्वारा पानी को पात्र R जुड़ा रहता है जिसे उदग्र स्टैण्ड पर ऊपर-नीचे खिसकाकर किसी भी स्थिति में स्थिर m किया जा सकता है। अनुनाद AB को एक दूसरी काँच की अनुनाद नली नली CD से रबर की छोटी नली की सहायता से जोड़ दिया जाता है। यह अनुनाद नली के समान्तर लगी होती है। इसी के समान्तर एक पैमाना S भी लगा हुआ होता है। नली CD में पानी के तल को देखकर अनुनाद नली में वायु स्तम्भ की लम्बाई पैमाने की सहायता से ज्ञात की जा सकती है।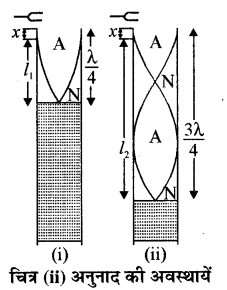
अनुनाद नली AB में इतना पानी भरा जाता है कि इसका (frac{2}{3}) भाग पानी से भरा रहे नली में पानी की सतह से उसके मुँह – तक के भाग में वायु स्तम्भ है। इस प्रकार से यह नली अब बन्द पाइप की तरह व्यवहार करती है। अब हम एक उच्च आवृत्ति का स्वरित्र लेकर उसे रबर के पैड पर मारकर अनुनाद नली के मुँह पर चित्र में दिखाये अनुसार रखते हैं। पात्र R को शनैः-शनैः नीचे अथवा ऊपर करते हैं। कम्पन करते हुए स्वरित्र द्वारा प्रणोदित कम्पन उत्पन्न होते हैं तथा नली में अनुदैर्ध्य अप्रगामी तरंगें बनती हैं। अनुनाद नली वायु स्तम्भ की लम्बाई को इस प्रकार समायोजित करते हैं कि नली में तीव्र ध्वनि सुनाई दे, यह अनुनाद की प्रथम अवस्था है। इस स्थिति में पानी के तल की स्थिति पैमाने की सहायता से पढ़कर वायु स्तम्भ की लम्बाई ज्ञात कर ली जाती है। माना कि यह लम्बाई l1 है। अतः अनुनाद की प्रथम स्थिति के लिए
l1 + x = (frac{lambda}{4}) ………..(1)
यहाँ x सिरा संशोधन कहलाता है। नली में बनी अप्रगामी तरंगों का प्रस्पन्द ठीक नली के सिरे पर नहीं बनकर सिरे से कुछ ऊपर x दूरी पर बनता है। [चित्र (i), (ii)] सिरा संशोधन का मान नली के आकार पर निर्भर करता है। प्रयोगों द्वारा यह पता किया जा चुका है कि इसका मान 0.3 D होता है, जहाँ D नली का व्यास है।
अब हम पात्र R को इतना नीचे करते हैं कि जब उसी स्वरित्र को कम्पित अवस्था में अनुनाद नली के मुँह पर ले जावें तो अनुनाद नली में पुनः तीव्र ध्वनि सुनाई दे। अनुनाद नली में अब वायु स्तम्भ की लम्बाई | प्रथम अनुनादी नली की तीन गुनी प्राप्त होती है। चित्र (ii) से अनुनाद की द्वितीय स्थिति के लिए।
l2 + x = (frac{3 lambda}{4})
समीकरण (2) में समीकरण (1) को घटाने पर
l2 + x – l1 – x =(frac{3 lambda}{4}-frac{lambda}{4}=frac{2 lambda}{4})
⇒ l2 – l1 = (frac{lambda}{2})
या λ = 2(l2 – l1) …………..(3)
यदि दिये गये स्वरित्र की आवृत्ति n है तो अनुनादित वायु स्तम्भ की भी यही आवृत्ति होगी। अतः वायु में ध्वनि का वेग v = nλ.
v = n × 2(l2 – l1)
v = 2n(l2 – l1) …………….(4)
यदि कमरे का ताप t°C है तो
vt = vo + 0.61 t ………… (5)
सिरा संशोधन (End Correction)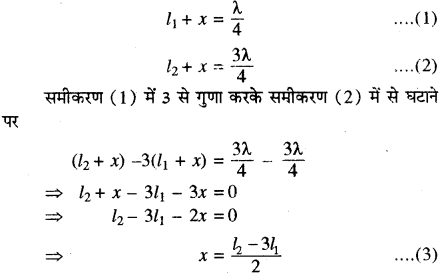
समीकरण (3) का उपयोग करके सिरा संशोधन ज्ञात किया जा सकता है।
प्रश्न 8.
विस्पन्द क्या है? गणितीय विश्लेषण द्वारा सिद्ध कीजिए कि प्रति सेकण्ड विस्पन्दों की संख्या स्रोतों की आवृत्ति में अन्तर के बराबर होती है।
उत्तर:
एक ही स्थान पर ध्वनि की तीव्रता में निश्चित समयान्तर में होने वाले नियमित उतार-चढ़ाव को ही विस्पन्द कहते हैं। चित्र के अनुसार, जब लगभग समान आवृत्ति की दो तरंगें एक ही दिशा में संचरित होती हुई माध्यम के किसी बिन्दु पर अध्यारोपित होती हैं तब वहाँ पर परिणामी तरंग का आयाम समय पर निर्भर करता है। जिसके कारण ध्वनि की तीव्रता में आवर्ती रूप से उतार-चढ़ाव होता है, इस घटना को विस्पन्द कहते हैं ।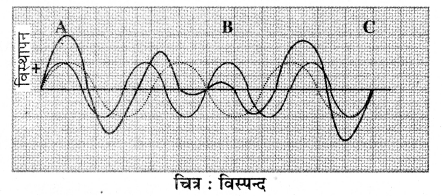
विस्पन्द आवृत्ति (n) प्रति सेकण्ड विस्पन्दों की संख्या विस्पन्द आवृत्ति कहलाती है।![]()
विस्पन्द काल (T) दो क्रमागत विस्पन्दों के मध्य समयान्तर को विस्पन्द काल कहते हैं।
माना दो स्वरित्र जिनकी आवृत्तियाँ n1 व n2 हैं एक साथ कम्पित कराये जाते हैं और इसमें आवृत्ति n1 का मान n2 से कुछ ही अधिक है। (अन्तर लगभग 10 आवृत्ति तक) है। कान पर ध्वनि करीब (left(frac{1}{12}right)) सेकण्ड तक रहती है अतः विस्पन्द तभी श्रव्य होंगे जब दो क्रमागत विस्पन्दों के बीच समयान्तर इससे अधिक होगा। जब n1 आवृत्ति वाला स्वरित्र n2 आवृत्ति वाले स्वरित्र से एक कम्पन अधिक कर लेगा तो एक विस्पन्द सुनाई देगा।
यदि विस्पन्द का आवर्तकाल T है तो इतने समय में यदि n1 आवृत्ति वाला स्वरित्र x कम्पन करता है तो n2 आवृत्ति वाला स्वरित्र (x – 1) कम्पन करेगा।
अर्थात् विस्पन्द की आवृत्ति दोनों स्वरित्रों की आवृत्ति के अन्तर के बराबर होती है।
विस्पन्द का गणितीय विश्लेषण (Mathematical Analysis of Beats) माना दो ध्वनि तरंगें जिनके आयाम क्रमशः a1 तथा a2 आवृत्तियाँ n1 तथा n2 हैं। एक ही दिशा में चलकर अध्यारोपण के पश्चात् किसी बिन्दु पर विस्पन्द उत्पन्न करती हैं। उन दोनों तरंगों को निम्न समीकरणों से प्रदर्शित किया जा सकता है
y1 = a1 sin 2πn1t
y2 = a2 sin 2πn2t ……………(2)
सरलता के लिए हमने इस बिन्दु पर x = 0 लिया है और यहाँ पर कलाएँ ϕ1 = ϕ2 = 0 हैं।
y = y1 + y2
y = a1 sin 2πn1t + a2 sin 2πn2t
माना n1 > n2 तथा n1 – n2 = Δn = n1 = n2 + Δn
यहाँ पर Δn अल्प आवृत्ति अन्तराल है।
y = a1 sin 2(πn2 + Δn)t + a2 sin (2πn2t)
y = a1 sin (πn2t + 2πΔnt) + a2 sin (2πn2t )
हम जानते हैं। sin(A + B) = sin A cos B + cos A sin B
y = a1 sin 2πn2t cos (2πΔnt) + a1 cos (2πn2t) × sin (2πΔnt) + a2 sin (2πn2t)
y = sin (2πn2t) [a1 cos (2πΔnt) + a2] + [a1 cos (2πn2t) × sin (2πΔnt)]
माना a1 cos (2πΔnt) + a2 = R cos α ………. (3)
a1 sin (2πΔnt) = R sin α …………(4)
∴ y = sin(2πn2t) [R cos α] + cos (2πn2t) (R sin α)
y = R [sin (2πn2t) cos α + cos (2πn2t) sin α]
y = R sin (2πn2t + α) …………. (5)
समीकरण (5) परिणामी तरंग का समीकरण है जिसका आयाम R है। समीकरण (3) तथा (4) का वर्ग करके जोड़ने पर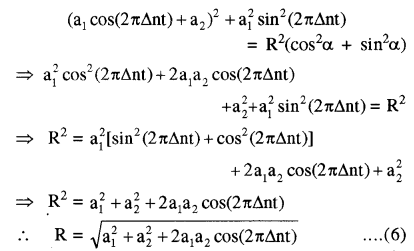
समीकरण (6) परिणामी तरंग के आयाम को व्यक्त करता है। इससे स्पष्ट है कि आयाम R का मान समय t के साथ बदलता है।
अतः जब t = 0, तब
R = a1 + a2 ध्वनि का आयाम अर्थात् तीव्रता अधिकतम
जब . t = (frac{1}{2 Delta n}) तब
R = a1 – a2 ध्वनि का आयाम अथवा तीव्रता न्यूनतम
जब t = (frac{2}{2 Delta n}), तब R = a1 + a2 ध्वनि की तीव्रता अधिकतम
जब t = (frac{3}{2 Delta mathrm{n}}) तब R = a1 – a2 ध्वनि की तीव्रता न्यूनतम
अतः परिणामी तरंग के कारण एक ही बिन्दु पर समय के साथ ध्वनि की तीव्रता में परिवर्तन होता रहता है। प्रारम्भ में (t = (frac{1}{2 Delta mathrm{n}})) ध्वनि की
तीव्रता अधिकतम तो कुछ समय पश्चा ध्वनि की तीव्रता न्यूनतम पुनः तीव्रता बढ़ती है तथा t = (frac{1}{Delta mathrm{n}}) पर तीव्रता पुनः अधिकतम हो जाती है।
∴ विस्पन्द का आवर्तकाल = दो क्रमागत अधिकतम ध्वनि की तीव्रता में लगा समय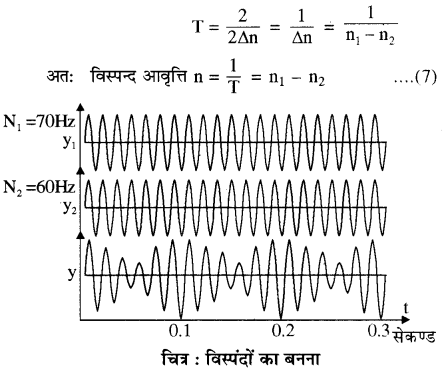
अर्थात् विस्पन्द आवृत्ति दोनों तरंगों की आवृत्ति के अन्तर के बराबर होती है। चित्र में एक तरंग की आवृत्ति 70 Hz तथा दूसरी तरंग की आवृत्ति 60 Hz है। अतः प्रति सेकण्ड 10 विस्पंद प्राप्त होंगे।
वैकल्पिक विधि
उपरोक्त समीकरणों (1) व (2) को निम्नानुसार भी लिखा जा सकता है
y1 = a1 sin ω1t तथा y2 = a2 sin ω2t
यदि दोनों तरंगों के आयाम समान लें तो ।
y1 = a sin ω1t तथा y2 = a sin ω2t
इन दोनों तरंगों के अध्यारोपण के फलस्वरूप
y = y1 + y2
= a [sin ω1t + sin ω2t]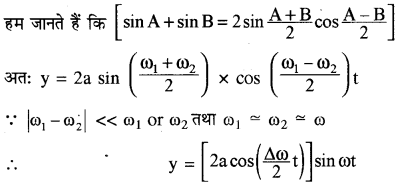

इससे स्पष्ट है कि (1 / Delta n)अन्तराल पर हमें अधिकतम ध्वनि सुनाई देती है।
अतः विस्पन्द आवृत्ति Δn होगी।
प्रश्न 9.
ध्वनि तरंगों में डाप्लर के प्रभाव की व्याख्या करो तथा आभासी आवृत्ति हेतु सूत्र ज्ञात करो जब
(i) स्रोत, स्थिर श्रोता की ओर गतिशील है।
(ii) श्रोता, स्थिर स्रोत की ओर गतिशील है।
उत्तर:
ध्वनि तरंगों (Doppler Effect is Sound Waves)
जब किसी स्थिर ध्वनि स्रोत (Source) से ध्वनि उत्पन्न होती है। तो उससे कुछ दूरी पर स्थित स्थिर श्रोता (Listener) को स्रोत से उत्पन्न ध्वनि की आवृत्ति में कोई परिवर्तन का आभास नहीं होता है। परन्तु जब ध्वनि स्रोत तथा श्रोता के बीच आपेक्षिक गति होती है तो श्रोता को ध्वनि की आवृत्ति में परिवर्तन प्रतीत होता है, इसे ‘डॉप्लर को प्रभाव’ कहते हैं। इस घटना का अध्ययन सर्वप्रथम सन् 1842 में ऑस्ट्रियन वैज्ञानिक जोहॉन डॉप्लर ने किया था। इस कारण इस प्रभाव को डॉप्लर प्रभाव कहते हैं।
डॉप्लर का प्रभाव निम्न चार परिस्थितियों में देखा जाता है
- जब ध्वनि स्रोत गतिमान हो तथा श्रोता स्थिर हो।
- जब श्रोता गतिमान हो तथा स्रोत स्थिर हो।
- जब स्रोत तथा श्रोता दोनों गतिमान हों।
- जब माध्यम (हवा) गतिमान हो।
डॉप्लर प्रभाव जब स्रोत गतिमान हो तथा श्रोता स्थिर हो।
(Doppler Effect when Source in Motion and Listener at Rest)
(i) जब स्रोत श्रोता की ओर गति करता है
चित्र (i) के अनुसार माना ध्वनि स्रोत S से उत्सर्जित तरंगों की वास्तविक आवृत्ति n, तरंगदैर्ध्य λ तथा ध्वनि का वेग v है।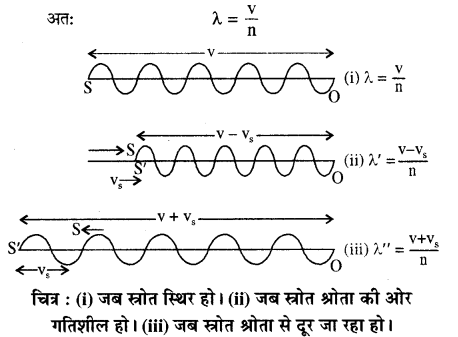
जब स्रोत एवं श्रोता दोनों स्थिर रहते हैं तब ध्वनि स्रोत से एक सेकण्ड में उत्सर्जित n तरंगें v मीटर की दूरी में प्रसारित हो जाती हैं एवं श्रोता प्रति सेकण्डे n तरंगें प्राप्त करेगा।
यदि स्रोत vs वेग से ध्वनि के वेग v की दिशा में गमन करे तो वह एक सेकण्ड में ध्वनि की दिशा में vs मीटर दूरी तय करेगा। अतः एक सेकण्ड में उत्सर्जित n तरंगें SO = V – vs दूरी में फैलेंगी।
चित्र (ii) अब ध्वनि की तरंगदैर्घ्य λ’ है तो
λ’ = (frac{mathbf{v}-mathbf{v}_{mathbf{S}}}{mathbf{n}})
इस स्थिति में आभासी तरंगदैर्घ्य वास्तविक तरंगदैर्ध्य से कम होती है। इस कारण श्रोता की ध्वनि की आवृत्ति बढ़ी हुई प्रतीत होगी।
यदि आभासी आवृत्ति n’ है तो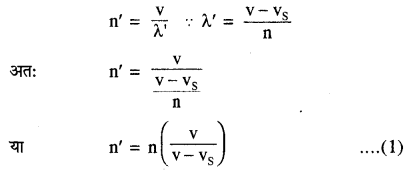
अतः आभासी आवृत्ति (n’) वास्तविक आवृत्ति (n) से अधिक होगी।
(ii) स्रोत स्थिर श्रोता से दूर जा रहा है
यदि ध्वनि स्रोत vs वेग से श्रोता से दूर जा रहा है तो स्रोत से प्रति सेकण्ड उत्सर्जित n तरंगें (v + vs) दूरी में फैलेंगी । चित्र (iii) से, अतः अब तरंगदैर्घ्य λ” हो जाये तो।
λ” = (frac{mathbf{v}+mathbf{v}_{mathbf{S}}}{mathbf{n}})
अर्थात् इस स्थिति में आभासी तरंगदैर्घ्य वास्तविक तरंगदैर्ध्य से अधिक होगी। इस स्थिति में ध्वनि स्रोत की आभासी आवृत्ति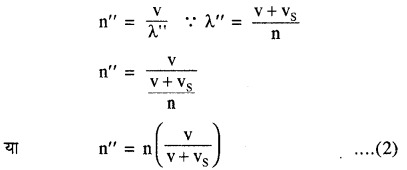
अतः आभासी आवृत्ति (n”) वास्तविक आवृत्ति (n) से कम | होगी।
(iii) स्रोत, स्थिर श्रोता के पास से गुजरता है
जब स्रोत vs वेग से स्थिर श्रोता की ओर आ रहा है तो आभासी आवृत्ति n’ = (nleft(frac{v}{v-v_{S}}right))
जब स्रोत vs वेग से स्थिर श्रोता को पार कर दूर जा रहा है तो आभासी आवृत्ति
n” = (nleft(frac{v}{v+v_{S}}right))
अतः आभासी आवृत्ति में परिवर्तन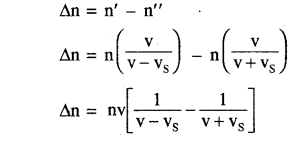
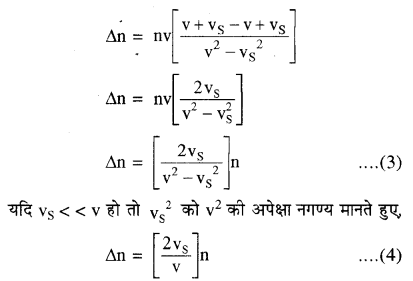
डॉप्लर प्रभाव जबकि श्रोता गतिशील तथा ध्वनि स्रोत
स्थिर हो (Doppler Effect when Listener in Motion and Source at Rest)
(i) श्रोता, ध्वनि स्रोत की ओर गतिशील है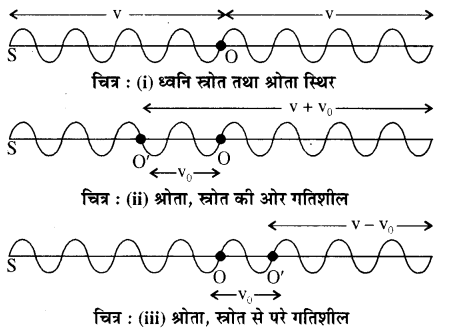
माना प्रारम्भ में ध्वनि स्रोत S व श्रोता O स्थिर है तो श्रोता एक सेकण्ड में स्रोत से आने वाली n तरंगें प्राप्त करता है। [चित्र (i)] । श्रोता एक सेकण्ड में vo दूरी स्रोत की ओर तय करके स्थिति O’ पर आ जाता है [चित्र (ii)] अतः अब वह n तरंगों के अतिरिक्त vo दूरी में स्थित Δn तरंगों को भी सुन सकेगा।
अतः श्रोता को एक सेकण्ड में प्राप्त होने वाली कुल तरंगों की संख्या अर्थात् आभासी आवृत्ति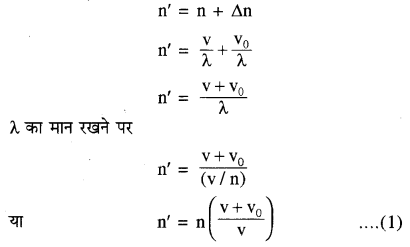
अतः इस स्थिति में आभासी आवृत्ति (n’) का मान वास्तविक आवृत्ति (n) से अधिक होगी।
(ii) श्रोता ध्वनि स्रोत से दूर जा रहा है
चित्र (iii) में श्रोता ध्वनि स्रोत से vo वेग से दूर जा रहा है अतः वह प्रति सेकण्ड Δn तरंगें कम प्राप्त करेगा। अतः इस स्थिति में श्रोता को एक सेकण्ड में प्राप्त होने वाली कुल तरंगों की संख्या अर्थात् आभासी आवृत्ति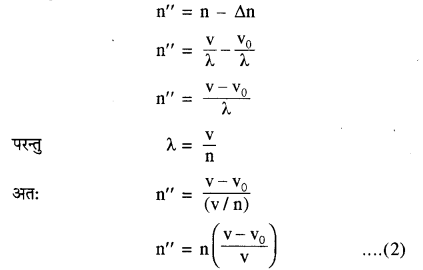
आभासी आवृत्ति (n”) का मान वास्तविक आवृत्ति (n) से कम होगा।
(iii) श्रोता; स्थिर स्रोत को पार करता है
जब श्रोता vo वेग से स्थिर स्रोत की ओर जा रहा है तो
RBSE Class 11 Physics Chapter 9 आंकिक प्रश्न
प्रश्न 1.
एकविमीय तरंग का अवकल समीकरण लिखिए तथा बताओ कि निम्न में से कौन-कौन से समीकरण एकविमीय तरंग के सम्भव हल हैं।
(i) y = 2 sin x cos vt
(ii) y = 5 sin 2x cos vt
हल:
(i) एकविमीय तरंग का अवकल समीकरण


अतः समीकरण y = 5 sin 2x cos vt समीकरण एकविमीय तरंग का सम्भव हल नहीं है।
प्रश्न 2.
500 हर्ट्ज की आवृत्ति का एक ध्वनि स्रोत वायु में अनुदैर्ध्य तरंगें उत्पन्न कर रहा है। तरंग में दो क्रमागत विरलनों के बीच की दूरी 0.64 मीटर है तथा वायु-कण के कम्पन का आयाम 0.002 मीटर है। इस तरंग का दूरी-विस्थापन समीकरण ज्ञात कीजिए। क्षण t=2 सेकण्ड पर तरंग की दिशा में मूल बिन्दु से 10 मीटर दूरी पर स्थित कण का विस्थापन ज्ञात कीजिए।
हल:
दिया है- n = 500 Hz
λ = 0.64 मीटर
आयाम a = 0.002 मीटर
y= a sin (Kx – ωt)
ω = 2πn
अतः कण का विस्थापन
= 1.402 × 10-3 मीटर = 1.402 मिमी.
अर्थात् यह मान (sqrt{2}) मिमी. के लगभग बराबर है।
प्रश्न 3.
एक डोरी पर चलती हुई तरंग का समीकरण निम्न है- y = 10 sin π (0.01x – 2.00t) जहाँ y तथा x cm में तथा t सेकण्ड में है। तरंग का आयाम, आवृत्ति तथा वेग ज्ञात कीजिए। किसी क्षण 40.0 cm की दूरी पर स्थित दो कणों के बीच कलान्तर ज्ञात कीजिए।
हल:
तरंग की समीकरण
y = 10 sin π (0.01x – 2.00 t)
y = 10 sin (0.01 πx – 2.00 πt)
यहाँ पर y तथा x को सेमी. में लिया गया है। प्रगामी तरंग का समीकरण
y = a sin (ωt – Kx) = – a sin (kx – ωt)
दिये गये तरंग समीकरण की तुलना प्रगामी तरंग के समीकरण से करने पर।
a = – 10 cm, ω = 2π रेडियन/सेकण्ड,
K = 0.01 π रेडियन/सेमी.
(i) तरंग का आयाम = 10 सेमी.
(ii) आवृत्ति
यहाँ पर ω = 2π
∴ 2πn = 2π
या n = 1 प्रति सेकण्ड
(iii) वेग
प्रश्न 4.
1.0 मीटर लम्बे खिंचे हुए स्टील के तार की मूल आवृत्ति 250 हर्ट्ज है। स्टील का घनत्व 8000 kg/m3 है। (i) तार में अनुप्रस्थ तरंग की चाल ज्ञात कीजिए (ii) तार के अनुदैर्ध्य प्रतिबल की गणना कीजिए (iii) यदि तार का तनाव 2% बढ़ा दिया जाए तो आवृत्ति में प्रतिशत परिवर्तन की गणना कीजिए।
हल:

यही आवृत्ति में प्रतिशत वृद्धि है।
प्रश्न. 5.
5.5 × 10 kg/m3 घनत्व की एक धातु में 400 कम्पन/सेकण्ड आवृत्ति की अनुदैर्ध्य तरंगों की तरंगदैर्घ्य ज्ञात करो। धातु का यंग प्रत्यास्थता गुणांक y = 8.8 × 1010 न्यूटन/मीटर2 है।
हल:
दिया है
घनत्व d = 5.5 × 103 kg/m3
आवृत्ति n = 400 Hz
y = 8.8 × 1010 न्यूटन/मीटर2
अतः आवृत्ति की तरंगदैर्घ्य λ = 10 मीटर
प्रश्न 6.
यदि एक तरंग का संचरण नियतांक 2.8 × 104 प्रति मीटर है और इसका वेग 400 मीटर प्रति सेकण्ड है तो तरंग के लिए तरंगदैर्घ्य, तरंग संख्या तथा तरंग आवृत्ति ज्ञात करो।
हल:
दिया है
K = 2.8 × 104 प्रति मीटर
v = 400 मीटर/सेकण्ड
इसलिए (lambda=frac{2 pi}{mathrm{K}}=frac{2 pi}{2.8 times 10^{4}})
प्रश्न 7.
5000 Å तरंगदैर्ध्य की प्रकाश तरंग की आवृत्ति, तरंग संख्या तथा संचरण नियतांक ज्ञात करो।
हल:
दिया है
प्रकाश तरंग ⇒ v = 3 × 108 मीटर/से.
λ = 5000 Å = 5 × 10-7 मीटर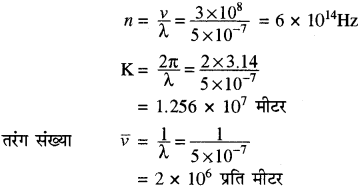
प्रश्न 8.
एक सरल आवर्ती तरंग 100 मीटर प्रति सेकण्ड के वेग से धनात्मक दिशा में जा रही है। तरंग का आयाम 2 cm तथा आवृत्ति 100 कम्पन सेकण्ड-1 (Hz) है।t = 5 सेकण्ड पर मूल बिन्दु से x = 2 मीटर पर किसी कण का विस्थापन, वेग तथा त्वरण ज्ञात करो।
हल:
दिया है
v = 100 मी./से.
आयाम a = 2 सेमी.
आवृत्ति n = 100 Hz और t = 5 सेकण्ड
ω = 2π = 2π × 100 = 200π
अब y = a sin (Kx – ωt) ……………. (1)
(frac{d y}{d t}) = v = – aω cos (Kr – ωt) ………….. (2)
(frac{d^{2} y}{d t^{2}}) = a(त्वरण) = aω2 sin (Kx – ωt) …..(3)
अब (v=frac{omega}{mathrm{K}} Rightarrow 100=frac{200 pi}{mathrm{K}})
∴ K = 2π
समीकरण (1) से
y = 0.02 sin (2πx – 200πt)
अब x= 2 और t = 5 पर
y” = 0.02 sin (2π × 2 – 200π × 5)
= 0.02 sin (4π – 1000π)
= 0.02 sin (- 996 π) = 0
∵ sin π = 0
समीकरण (2) से
v = – aω cos (2π × 2 – 200π × 5)
= – aω cos (4π – 1000π)
= – aω cos (- 996π) = – aω cos 996π
∵ cos 996π = 1
= – aω × 1 = – aω
v = – aω = — 0.02 × 200π
मापांक लेने पर
(|v|) = 4π = 4 × 3.14 = 12.56 मी./से.
समीकरण (3) से
त्वरण (a) = aω2 sin (Kx – ωt)
= aω2 sin (2π × 2 – 200π ×5)
= aω2 sin (- 996π ) = 0
अतः त्वरण (a) = शून्य
प्रश्न 9.
50 मीटर लम्बे 10 kg भार से खींचे गए तार के मूल स्वर की आवृत्ति ज्ञात करो जबकि 1 मीटर लम्बे तार का भार 2.45 ग्राम है। (g = 980 cm/s2 सेमी./सेकण्ड2)
हल:
दिया है
द्रव्यमान M= 10 kg
तार में तनाव T= Mg
= (10 kg) × 9.8 m/s2
= 98N
m = एकांक लम्बाई का द्रव्यमान
= 2.45 gm
= 2.45 × 10-3 kg
वेग v = (sqrt{frac{mathrm{T}}{m}}=sqrt{frac{98}{2.45 times 10^{-3}}}) m/s
= 200 m/s
अतः आवृत्ति n = (frac{v}{lambda})
= (frac{200 mathrm{m} / mathrm{s}}{1}) ∵ λ = 1 मीटर
= 200 Hz
प्रश्न 10.
100 cm लम्बा और 1.8 mm व्यास वाला तांबे का तार (घनत्व 8.4) 20 kg भार से खींचा गया है। मूल स्वर से कम्पन होने पर इसकी आवृत्ति ज्ञात करो।
हल:
दिया है
l = 100 cm
त्रिज्या r = (frac{1.8}{2}) mm = 0.9 mm = 9 × 10-2 cm
g = 980 cm/sec2, घनत्व d = 8.4
M = 20 kg = 20000 g
हम जानते हैं
n = (frac{1}{2 l} sqrt{frac{T}{pi r^{2} d}})
मान रखने पर
प्रश्न 11.
एक स्वरित्र द्विभुज के स्वर में और 25 cm खींचे हुए तार के स्वर में स्वरैक्य है। यदि तार की लम्बाई बदल कर 25.5 cm कर दी जाये तथा तनाव वही रहने पर 3 विस्पन्द प्रति सेकण्ड उत्पन्न होते हैं। स्वरित्र की आवृत्ति ज्ञात करो।
हल:
माना कि स्वरित्र की आवृत्ति n है तब स्वर मेल की स्थिति में
n = (frac{1}{2 l} sqrt{frac{T}{m}})
n= (frac{1}{2 times 25} sqrt{frac{mathrm{T}}{m}}) …………(1)
लम्बाई बढ़ाने पर अब तार की लम्बाई = 25.5 सेमी. है। तार की लम्बाई बढ़ाने पर तार की आवृत्ति कम हो जायेगी अर्थात् (n = 3) हो जायेगी अतः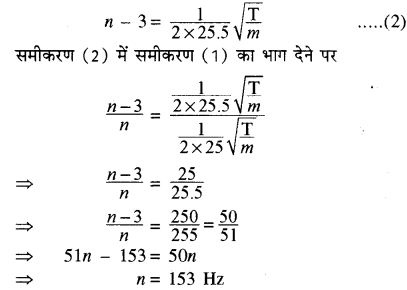
प्रश्न 12.
एक सोनोमीटर तार 150 आवृत्ति वाला स्वर देता है। यदि तार का तनाव 9 : 16 के अनुपात में व लम्बाई 1 : 2 के अनुपात में बदली जाये तो तार की नई आवृत्ति ज्ञात करो।
हल:
दिया है— n1 = 150 Hz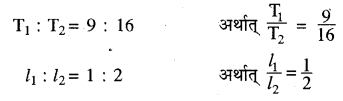
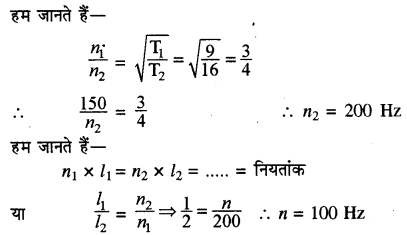
प्रश्न 13.
दोनों सिरों पर बद्ध डोरी के अनुप्रस्थ कम्पन का समीकरण y = (x, t) = 0.3 sin((frac{2 pi}{3} x)) cos (120π t) है। जहाँ y तथा मीटर में तथा ‘सेकण्ड में है। डोरी की लम्बाई 1.5 मीटर तथा द्रव्यमान 0.002 kg है तो
(i) x = 0.5 मीटर पर अधिकतम विस्थापन ज्ञात करो
(ii) तार पर निस्पन्दों के स्थान का निर्धारण करो।
(iii) तरंग वेग ज्ञात करो।
(iv) x = 0.75 मीटर तथा t = 0.25 सेकण्ड पर स्थित कण का वेग ज्ञात करो।
हल:
प्रश्नानुसार, अनुप्रस्थ कम्पन का समीकरण
चूँकि डोरी की लम्बाई 1.5 मीटर है इसलिए डोरी के दोनों सिरों पर ही निस्पंद बनते हैं।
(iii) तरंग वेग v = nλ
प्रश्न 14.
41 स्वरित्रों को इस प्रकार व्यवस्थित किया जाता है कि प्रत्येक स्वरित्र अपने समीप के स्वरित्र से 5 विस्पन्द/सेकण्ड उत्पन्न करता है। अन्तिम स्वरित्र की आवृत्ति प्रथम स्वरित्र की आवृत्ति से दुगुनी है। प्रथम एवं अन्तिम स्वरित्रों की आवृत्ति ज्ञात करो।
हल:
दिया गया है-स्वरित्रों की संख्या = 41
प्रत्येक स्वरित्र के बीच में 5 विस्पन्द प्रति सेकण्ड उत्पन्न करता है।
अन्तिम स्वरित्र की आवृत्ति = 2 × प्रथम स्वरित्र की आवृत्ति
माना प्रथम स्वरित्र की आवृत्ति = x कम्पन/सेकण्ड
यहाँ पर समान्तर श्रेणी बन रही है
x, x + 5, x + 10, …… x + 40d
n = 41 है।
x + 40d = 2 × (3)
⇒ x = 40d
a = 5 विस्पन्द/सेकण्ड
∴ x = 40 × 5 = 200 Hz
∴ x41 = x + 40d = 200 + 40 × 5
= 200 + 200 = 400 Hz.
प्रश्न 15.
ध्वनि के वेग को उस गैस में ज्ञात करो जिसमें 1 व 1.01 मीटर तरंगदैर्घ्य वाली दो तरंगें 3 सेकण्ड में 10 विस्पन्द पैदा करती हैं।
हल:
माना गैस में तरंगों का वेग v मीटर/सेकण्ड है।
इसलिए पहली तरंग की आवृत्ति
∴ (frac{v}{101}=frac{10}{3})
या v = (frac{10 times 101}{3}=frac{1010}{3}) = 336.7 मी./से.
प्रश्न 16.
उस स्वरित्र की आवृत्ति ज्ञात करो जिसे 256 की आवृत्ति वाले स्वरित्र द्विभुज के साथ बजाने पर 6 विस्पन्द प्रति सेकण्ड तथा 253 आवृत्ति वाले स्वरित्र के साथ बजाने पर 3 विस्पन्द प्रति सेकण्ड उत्पन्न होते हैं।
हल:
पहली अवस्था के अनुसार आवृत्ति
n’ = 256 ± 6 = 262 या 250
दूसरी अवस्था के अनुसार आवृत्ति
n’ = 253 ± 3 = 256 या 250
अतः दोनों अवस्थाओं के परिणामों को सन्तुष्ट करने के लिए अज्ञात आवृत्ति 250 Hz होनी चाहिए।
प्रश्न 17.
एक स्वरित्र स्वरमापी के खिंचे हुए तार की 0.49 मीटर एवं 0.50 मीटर लम्बाइयों में प्रत्येक से 4 विस्पन्द प्रति सेकण्ड उत्पन्न करता है। स्वरित्र की आवृत्तियाँ ज्ञात कीजिए।
हल:
माना स्वरित्र की आवृत्ति = n Hz है।
लम्बाई के नियम के अनुसार किसी कम्पित तार की आवृत्ति n उसकी लम्बाई l के व्युत्क्रमानुपाती होती है, अर्थात् n ∝ (frac{1}{l}) अतः तार की लम्बाई अधिक लम्बाई l1 = 0.50 मीटर = 50 सेमी. पर तार की कम आवृत्त n1 = (n – 4) तथा तार की कम लम्बाई l2 = 0.49 मीटर = 49 सेमी. पर तार की अधिक आवृत्ति n2 = (a +4) होगी (चूंकि स्वरित्र तार की इन दोनों लम्बाइयों के साथ 4 विस्पन्द प्रति सेकण्ड देता | है।)
∵ लम्बाई के नियम के अनुसार, n ∝ (frac{1}{l}) अर्थात्
nl= नियतांक अर्थात् n1 × l1 = n2 × l2
∴ (n – 4) × 50 = (n × 4) × 49
अथवा 50n – 200 = 49n + 196 अर्थात्
n = 196 + 200 = 396 Hz
प्रश्न 18.
दो इंजन एक-दूसरे के पास से विरुद्ध दिशा में गुजरते हैं। एक इंजन 540 आवृत्ति वाली सीटी बजाता है। दूसरे इंजन में बैठे लोग एक-दूसरे से गुजरने के पहले और बाद में कौनसी आवृत्ति की सीटी सुनेंगे? दोनों इंजनों का वेग 40 मीटर प्रति सेकण्ड है। ध्वनि का वेग 340 मीटर/सेकण्ड है।
हल:
इंजनों के वेग = 40 मीटर/सेकण्ड
जब इंजन एक-दूसरे की ओर गति करते हैं तो एक इंजन के सीटी बजाने से एक ध्वनि स्रोत व दूसरे का चालक प्रेक्षक बन जाता है। इस दशा में आभासी आवृत्ति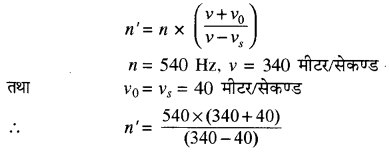
n’ = (frac{540 times 380}{300}) = 684 Hz
तथा जब वे एक-दूसरे को पार कर लेते हैं तो वे एक-दूसरे से दूर दिशा में गति करने लगते हैं। अतः इस अवस्था में आभासी आवृत्ति
n’= (nleft(frac{v-v_{0}}{v+v_{s}}right))
= (frac{540 times(340-40)}{(340+40)}=frac{540 times 300}{380})
= 426.315 Hz
प्रश्न 19.
एक ट्रेन 60 km/h के वेग से एक साइरन की ओर जा रही है जिसकी ध्वनि की आवृत्ति 400 कम्पन प्रति सेकण्ड है। ट्रेन में बैठे यात्री किस आवृत्ति की ध्वनि सुनेंगे?(हवा में ध्वनि का वेग 340 मीटर/सेकण्ड)
हल:
यहाँ स्रोत (रेल इंजन) की चाल
vs = 60 km/h
प्रश्न 20.
किसी इंजन की सीटी के स्वर की आवृत्ति उस समय 5/6 वां हिस्सा प्रतीत होती है जबकि वह स्थिर श्रोता को पार करता है। यदि ध्वनि का वायु में वेग 330 मीटर/सेकण्ड हो तो इंजन की गति ज्ञात कीजिये।
हल:
जब इंजन श्रोता की ओर आता है तो आभासी आवृत्ति
n’ = (left(frac{v}{v-v_{s}}right) n) …………(1)
जब इंजन श्रोता को पार कर उससे दूर जाता है तो आभासी आवृत्ति
n” = (left(frac{v}{v-left(-v_{s}right)}right) n=left(frac{v}{v+v_{s}}right) n) …………. (2)
(ध्वनि गमन की दिशा में वेग धनात्मक है)
समीकरण (2) में (1) का भाग देने पर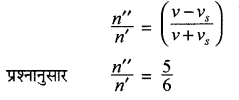
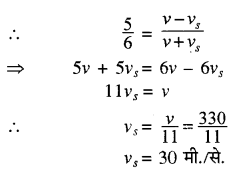
All Chapter RBSE Solutions For Class 12 Physics Hindi Medium
—————————————————————————–
All Subject RBSE Solutions For Class 11 Hindi Medium
*************************************************
————————————————————
All Chapter RBSE Solutions For Class 11 physics Hindi Medium
All Subject RBSE Solutions For Class 11 Hindi Medium
Remark:
हम उम्मीद रखते है कि यह RBSE Class 11 physics Solutions in Hindi आपकी स्टडी में उपयोगी साबित हुए होंगे | अगर आप लोगो को इससे रिलेटेड कोई भी किसी भी प्रकार का डॉउट हो तो कमेंट बॉक्स में कमेंट करके पूंछ सकते है |
यदि इन solutions से आपको हेल्प मिली हो तो आप इन्हे अपने Classmates & Friends के साथ शेयर कर सकते है और HindiLearning.in को सोशल मीडिया में शेयर कर सकते है, जिससे हमारा मोटिवेशन बढ़ेगा और हम आप लोगो के लिए ऐसे ही और मैटेरियल अपलोड कर पाएंगे |
आपके भविष्य के लिए शुभकामनाएं!!