हेलो स्टूडेंट्स, यहां हमने राजस्थान बोर्ड Class 11 Physics Chapter 7 दृढ़ पिण्ड गतिकी सॉल्यूशंस को दिया हैं। यह solutions स्टूडेंट के परीक्षा में बहुत सहायक होंगे | Student RBSE solutions for Class 11 Physics Chapter 7 दृढ़ पिण्ड गतिकी pdf Download करे| RBSE solutions for Class 11 Physics Chapter 7 दृढ़ पिण्ड गतिकी notes will help you.
Table of Contents
Rajasthan Board RBSE Class 11 Physics Chapter 7 दृढ़ पिण्ड गतिकी
RBSE Class 11 Physics Chapter 7 पाठ्य पुस्तक के प्रश्न एवं उत्तर
RBSE Class 11 Physics Chapter 7 अतिलघूत्तरात्मक प्रश्न
प्रश्न 1.
दृढ़ पिण्ड किसे कहते हैं?
उत्तर:
ऐसे पिण्ड जिन पर बाह्य बल लगाने पर कणों के मध्य की दूरियाँ अपरिवर्तित रहती हों, दृढ़ पिण्ड कहलाते हैं।
प्रश्न 2.
द्रव्यमान केन्द्र की परिभाषा दीजिये।
उत्तर:
द्रव्यमान केन्द्र वह बिन्दु है जिसके परितः सभी कणों के द्रव्यमान आघूर्गों का योग शून्य होता है।
प्रश्न 3.
क्या किसी पिण्ड का द्रव्यमान केन्द्र, पिण्ड के बाहर हो सकता है?
उत्तर:
हाँ, जैसे वलय इत्यादि।
प्रश्न 4.
किसी निकाय के रेखीय वेग एवं कोणीय वेग में सम्बन्ध लिखिये।।
उत्तर:
(vec{v}=vec{omega} times overrightarrow{mathrm{R}})
प्रश्न 5.
हाथ की एक घड़ी के मिनट वाली काँटे की कोणीय चाल rad s-1 में क्या होती है?
उत्तर:
(omega=frac{2 pi}{mathrm{T}}=frac{2 pi}{3600}=frac{pi}{1800}) rad s-1
प्रश्न 6.
जड़त्व आघूर्ण से क्या अभिप्राय है?
उत्तर:
किसी पिण्ड का वह गुण जिसके कारण वह किसी अक्ष के परितः घूर्णन में किये जाने वाले परिवर्तन का विरोध करता है, पिण्ड का घूर्णन अक्ष के परितः जड़त्व आघूर्ण कहलाता है।
प्रश्न 7.
किसी वस्तु का जड़त्व आघूर्ण किन-किन घटकों पर निर्भर करता है?
उत्तर:
घूर्णन अक्ष की स्थिति, पिण्ड के द्रव्यमान एवं द्रव्यमान वितरण पर
प्रश्न 8.
एक वलय का उसके व्यास के सापेक्ष जड़त्व आघूर्ण कितना होता है?
उत्तर:
Id = (frac{mathrm{MR}^{2}}{2})
प्रश्न 9.
किसी चकती के जड़त्व आघूर्ण का मान न्यूनतम किस अक्ष के प्रति होता है?
उत्तर:
उसके व्यास के सापेक्ष।
प्रश्न 10.
किसी ठोस गोले का उसके स्पर्श रेखा के सापेक्ष घूर्णन क्रिज्या का मान लिखिये।
उत्तर:
K = (mathrm{R} sqrt{frac{7}{5}})
प्रश्न 11.
कोणीय संवेग की इकाई लिखिये।
उत्तर:
Kg m2s-1 या Js
प्रश्न 12.
एक व्यक्ति घूमती मेज पर भुजायें फैलाये बैठा है, अगर वह भुजायें सिकोड़ ले तो जड़त्व आघूर्ण पर क्या प्रभाव पड़ेगा?
उत्तर:
जड़त्व आघूर्ण घट जायेगा।
प्रश्न 13.
यदि कोणीय संवेग में परिवर्तन की दर शून्य हो तो पिण्ड पर कार्यकारी बल आघूर्ण का मान क्या होगा?
उत्तर:
τ = 0 (शून्य)
प्रश्न 14.
यदि कोई वस्तु घूर्णन कर रही है तो क्या निश्चित रूप से उस पर कोई बल आघूर्ण लग रहा है?
उत्तर:
आवश्यक नहीं कि वस्तु पर निश्चित रूप से कोई बल आघूर्ण लग रहा है।
प्रश्न 15.
बल आघूर्ण, जड़त्व आघूर्ण व कोणीय त्वरण के मध्य सम्बन्ध को लिखिये।
उत्तर:
τ = Iα
प्रश्न 16.
पेचकस का हत्था चौड़ा क्यों बनाया जाता है?
उत्तर:
चूँकि τ = Fr = नियत अर्थात् F ∝ (frac{1}{r})
हत्था चौड़ा बनाने से घूर्णन अक्ष से लम्बवत् दूरी बढ़ जाने के कारण निश्चित बलाघूर्ण के लिए कम बल लगाने की आवश्यकता होती है।
प्रश्न 17.
यदि कोई वस्तु अपनी अक्ष के परितः घूमने के साथसाथ सरल रेखा में भी गतिमान हो तो उसकी कुल गतिज ऊर्जा का मान लिखिये।
उत्तर:
Ttotal = ELin + Erot
(mathrm{E}_{mathrm{Tot}}=frac{1}{2} mathrm{M} v^{2}+frac{1}{2} mathrm{I} omega^{2})
प्रश्न 18.
नत तल पर लोटनी गति करते पिण्ड का वेग का सूत्र लिखिये।
उत्तर:
v = (sqrt{frac{2 g h}{left(1+frac{K^{2}}{R^{2}}right)}})
प्रश्न 19.
दृढ़ पिण्डों के यांत्रिक संतुलन की शर्ते लिखिये।
उत्तर:
(sum_{i=1}^{n} overrightarrow{mathrm{F}}_{i}=0) तथा (sum_{i=1}^{n} vec{tau}_{i}=0)
प्रश्न 20.
कोणीय संवेग, जड़त्व आघूर्ण एवं कोणीय वेग के । सम्बन्ध को लिखिये।
उत्तर:
J = Iω
प्रश्न 21.
यदि पृथ्वी का व्यास सिकुड़कर आधा रह जाये तो दिन कितने घंटे का होगा?
उत्तर:
6 घण्टे रह जायेगा
RBSE Class 11 Physics Chapter 7 लघूत्तरात्मक प्रश्न
प्रश्न 1.
किसी द्विकण तंत्र के द्रव्यमान केन्द्र के लिये द्रव्यमाने एवं दूरी में सम्बन्ध स्थापित कीजिये।
उत्तर:
माना दो कण हैं जिनके द्रव्यमान क्रमशः m1 तथा m2 हैं तथा निर्देश बिन्दु O से स्थिति सदिश (vec{r}_{1}) व (vec{r}_{2}) एवं इन कणों का आपस में तथा बाह्य वातावरण से सम्बन्ध है।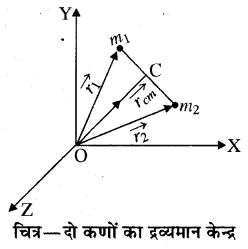
माना कि प्रथम कण पर द्वितीय कण द्वारा लगने वाला आन्तरिक बल (overrightarrow{mathrm{F}}_{1}^{prime}) तथा बाह्य बल (overrightarrow{mathrm{F}_{1}^{prime prime}}) कार्यरत है तो कण m1 पर लगने वाला परिणामी बल
(overrightarrow{mathrm{F}_{1}}=overrightarrow{mathrm{F}_{1}^{prime}}+overrightarrow{mathrm{F}_{1}^{prime prime}})
न्यूटन के द्वितीय नियम से कण पर लगने वाला बल उसके संवेग में परिवर्तन की दर के बराबर होता है।
(frac{d overrightarrow{p_{1}}}{d t}=overrightarrow{mathrm{F}_{1}})
इसी प्रकार द्वितीय कण के संवेग में परिवर्तन की दर
(frac{d overrightarrow{p_{2}}}{d t}=overrightarrow{mathrm{F}_{2}})
अतः दोनों कणों के लिए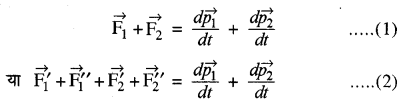
परन्तु न्यूटन के तृतीय नियम से दोनों कणों के मध्य आन्तरिक बल बराबर तथा विपरीत दिशा में कार्य करेंगे। अतः दोनों आन्तरिक बल एक-दूसरे को नष्ट कर देंगे।

प्रश्न 2.
रेखीय वेग एवं कोणीय वेग में सदिश सम्बन्ध स्थापित कीजिये।
उत्तर:
जब कोई दृढ़ पिण्ड अपनी स्थिर अक्ष के प्रति घूर्णन करता है तो उसका प्रत्येक कण वृत्ताकार पथ में गति करता है। प्रत्येक वृत्त घूर्णन तल में स्थित होता है जो घूर्णन अक्ष के लम्बवत् तथा अक्ष पर केन्द्रित होता है। शुद्ध घूर्णी गति में पिण्ड का प्रत्येक कण समान कोणीय वेग से घूमता है। कण की चाल का मान उसके कोणीय वेग के अनुक्रमानुपाती होता है। चित्र में दृढ़ पिण्ड का कण P, r त्रिज्या के वृत्ताकार पथ में घूर्णन गति कर रहा है। यदि किसी क्षण उसका कोणीय विस्थापन θ रेडियन हो तो चाप लम्बाई s को निम्न प्रकार से व्यक्त कर सकते हैं
S = rθ
r को स्थिर मानते हुए उपरोक्त समीकरण का समय के प्रति अवकलन करने पर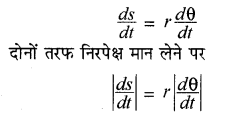
यहाँ (left|frac{d s}{d t}right|) चाप लम्बाई की लम्बाई में निरपेक्ष परिवर्तन की दर को व्यक्त करता है जो तात्क्षणिक रेखीय वेग (v) के तुल्य होता है तथा (left|frac{d theta}{d t}right|) तात्क्षणिक कोणीय वेग होगा। अतः
v = ωr ……………..(1)
स्पष्ट है कि जो कण दृढ़ पिण्ड के घूर्णन अक्ष से अधिक दूरी पर होगा उसका रेखीय वेग भी उतना ही अधिक होगा।
उपरोक्त सम्बन्ध को सदिश गुणनफल में निरूपित करने के लिये माना कण P का t = 0 पर स्थिति सदिश (overrightarrow{mathrm{R}}=overrightarrow{mathrm{OP}}) है। अतः चित्र से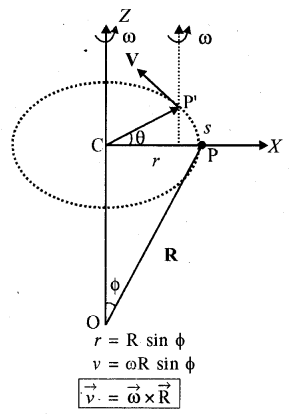
प्रश्न 3.
घूर्णन गति की तीन समीकरणों को लिखिये। :
उत्तर:
ω = ω0 + αt
θ = ω0t + (frac{1}{2})αt2
ω2 = ω02 + 2αθ
प्रश्न 4.
जड़त्व आघूर्ण के लिये लम्बवत् अक्ष का कथन दीजिये।
उत्तर:
कथन-किसी समतल पटल (Plane lamina) का उसके तल के लम्बवत् अक्ष के सापेक्ष जड़त्व-आघूर्ण उसके तल में स्थित दो परस्पर लम्बवत् अक्षों के सापेक्ष जड़त्व-आघूर्णो के योग के बराबर होता है जबकि अभीष्ट अक्ष उन दोनों अक्षों Vz के कटान बिन्दु से होकर गुजरती है।
प्रश्न 5.
जड़त्व आघूर्ण की समान्तर अक्ष प्रमेय को लिखिये।
उत्तर:
किसी घूर्णन अक्ष के सापेक्ष किसी पिण्ड का जड़त्व आघूर्ण (I), पिण्ड के गुरुत्व केन्द्र से गुजरने वाली समान्तर अक्ष के सापेक्ष पिण्ड के जड़त्व आघूर्ण (IG) तथा उसका द्रव्यमान (M) तथा दोनों समान्तर अक्षों के मध्य की दूरी (d) के वर्ग के गुणनफल के योगफल के बराबर होता है। अर्थात्
I = IG + Md2
प्रश्न 6.
वलय के केन्द्र से गुजरने वाली उसके तल के लम्बवत् अक्ष के सापेक्ष जड़त्व आघूर्ण ज्ञात कीजिये।
उत्तर:
माना M द्रव्यमान तथा R त्रिज्या की वलय है। जिसका केन्द्र O है। वलय का ZZ’ अक्ष के सापेक्ष जड़त्व आघूर्ण ज्ञात करना है।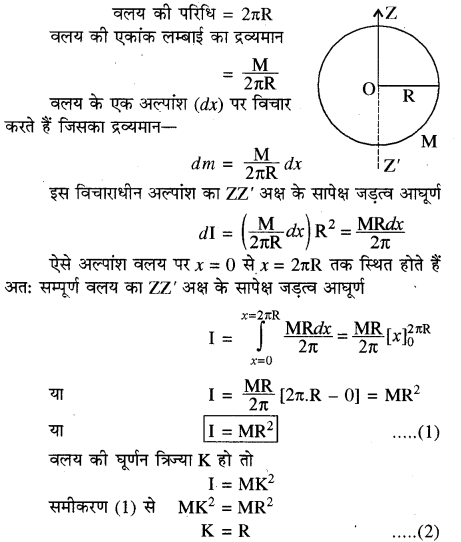
प्रश्न 7.
ठोस बेलन का उसके अक्ष के सापेक्ष जड़त्व आघूर्ण ज्ञात कीजिये।
उत्तर:
चित्रानुसार माना एक ठोस बेलन जिसका द्रव्यमाने M तथा त्रिज्या R है, XX’ इसकी घूर्णन अक्ष है जो कि बेलन की अपनी ज्यामितीय अक्ष से सम्पातित है, ठोस बेलन को उसके ज्यामितीय अक्ष के अनुदिश अनेक समाक्षीय चकतियों में सतत रूप से विभाजित किया जा सकता है।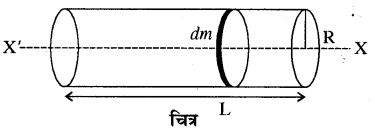
एक चकती जिसका द्रव्यमान (dm) है घूर्णन अक्ष XX’ के परितः जड़त्व आघूर्ण का मान
= (frac{1}{2}) (dm) R2
बेलन का कुल जड़त्व आघूर्ण इन चकतियों के XX’ के परितः जड़त्व आघूर्णो के योग के तुल्य होगा।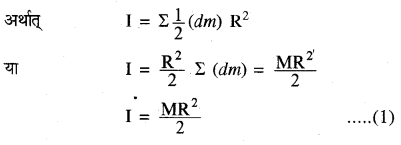
घूर्णन क्रिया K = (frac{mathrm{R}}{sqrt{2}}) ∵ K = (sqrt{frac{mathrm{I}}{mathrm{M}}}) …………….. (2)
प्रश्न 8.
किसी पिण्ड के लिये बल आघूर्ण एवं जड़त्व आघूर्ण में सम्बन्ध स्थापित कीजिये।
उत्तर:
चित्र में दर्शाये अनुसार अक्ष OO’ पर घूर्णन गति करते हुए पिण्ड पर विचार करते हैं जो कि एक तल के लम्बवत् वामावर्त दिशा में घूम रहा है।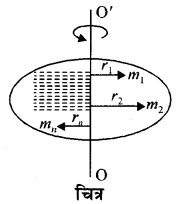
माना n कणों के द्रव्यमान क्रमशः m1, m2, m3,…….mn हैं। उनकी घूर्णन अक्ष से लम्बवत् दूरियाँ क्रमशः r1, r2……….rn, हैं। इन कणों पर लम्बवत् कार्य करने वाले बल क्रमशः F1, F2, F3,……Fn, हैं। माना पिण्ड का कोणीय त्वरण α है जो कि सभी कणों का समान है लेकिन रैखिक त्वरण a है जो कि समान नहीं है। m द्रव्यमान वाले कण पर लगने वाला बल F1, है
F1 = m1a1
अक्ष OO’ के सापेक्ष F1 का बल आघूर्ण,
τ1 = F1r1 = m1a1r1
परन्तु a1 = r1α
τ1 = m1r1αr1
τ1 = m1r12α
इसी प्रकार से अन्य कणों के लिये,
τ2 = m2r22α
τ3 = m3r32α
……………….
………………
………………
τn = mnrn2α
चूँकि सभी बल आघूर्ण एक ही दिशा में कार्य कर रहे हैं अतः परिणामी बल आघूर्ण
τ = τ1 + τ2 + τ3 +……..τn,
= m1r12α + m2r22α + …………………….. + mnrn2α
τ = α (m1r12 + m2r22 + ……….. + mnrn2
τ = αI
जहाँ पर जड़त्व आघूर्ण ।
I = m1r12 + m2r22+ ……. + mnrn2
सदिश रूप में (vec{tau}=I vec{alpha}) …………….(1)
अर्थात् किसी पिण्ड का किसी अक्ष के सापेक्ष बल आघूर्ण, उस अक्ष के सापेक्ष जड़त्व आघूर्ण तथा उसमें उत्पन्न कोणीय त्वरण के गुणनफल के बराबर होता है। यही घूर्णन गति की प्रधान समीकरण होती है।
यदि कोणीय त्वरण α = 1 रेडियन/से.2 हो तो
I = τ
इस प्रकार, किसी वस्तु का घूर्णन अक्ष के सापेक्ष जड़त्व आघूर्ण, वस्तु में उस अक्ष के सापेक्ष एकांक कोणीय त्वरण उत्पन्न करने के लिए आवश्यक बल आघूर्ण के बराबर होता है।
प्रश्न 9.
कोणीय संवेग संरक्षण नियम को लिखिये। इस पर आधारित दो उदाहरण लिखिये।
उत्तर:
कोणीय संवेग संरक्षण के सिद्धान्त के अनुसार बाह्य बल आघूर्ण की अनुपस्थिति में प्रत्येक कण, निकाय अथवा पिण्ड का कोणीय संवेग नियत रहता है।
किसी पिण्ड के लिये यदि बल आघूर्ण (vec{tau}=frac{overrightarrow{d mathrm{L}}}{d t})
अतः यदि (vec{tau}) तो (frac{overrightarrow{d mathrm{L}}}{d t}) = 0 जिससे (overrightarrow{mathrm{L}}) = नियतांक
यदि कोई पिण्ड कोणीय वेग ω से घूर्णी गति कर रहा है तथा घूर्णन अक्ष के सापेक्ष उसका जड़त्व आघूर्ण I है, तो L = Iω
बाह्य बल आघूर्ण लगाये बिना यदि जड़त्व आघूर्ण परिवर्तित होकर I’ हो जाता है तो उसका कोणीय वेग इस प्रकार परिवर्तित हो जायेगा कि कोणीय संवेग नियत बना रहे। यदि परिवर्तित कोणीय वेग ω’ है तो कोणीय संवेग संरक्षण सिद्धान्त से
Ioω = I’ω’
कोणीय संवेग संरक्षण का सिद्धान्त भी रेखीय संवेग संरक्षण के सिद्धान्त की भाँति भौतिकी का एक मूल सिद्धान्त है।
उदाहरण— (1) एक धागे के सिरे पर गेंद बाँध कर तथा इसका दूसरा सिरी एक ऊर्ध्वनली में से निकालकर हाथ में पकड़कर गेंद को तेजी से क्षैतिज वृत्त में घुमाया जाता है। यदि हम धागे को खींचकर वृत्तीय पथ की त्रिज्या को कम कर दें तो हम देखते हैं कि गेंद पहले की अपेक्षा तेजी से घूमती है। इसका कारण यह है कि त्रिज्या कम हो जाने के कारण गेंद का जडत्व आघूर्ण भी कम हो जाता है। और उसका कोणीय वेग बढ़ जाता है। (2) जब एक गोताखोर अपने हाथ फैलाये हुए किसी कोणीय वेग से छलाँग लगाता है तो वह बिना घूर्णन किये हुए जले में पहुँच जाता है परन्तु जब वह अपना घूर्णन बढ़ाना चाहता है तो उसको अपना जड़त्व आघूर्ण कम करना पड़ेगा। इसके लिये वह अपने हाथों और शरीर को सिकोड़ता है। पानी को छूने से पहले वह फिर से अपने हाथों और शरीर को फैलाकर अपने कोणीय वेग को कम करता है। इस स्थिति में उसका शरीर द्रव्यमान केन्द्र के चारों ओर अक्ष पर घूर्णन करता है एवं शरीर को द्रव्यमान केन्द्र एक प्रक्षेप्य के परवलीये पथ पर गमन करता है।
प्रश्न 10.
एक पिण्ड जो एक समान कोणीय वेग से एक स्थिर अक्ष के चारों ओर घूर्णन करता है, की गतिज ऊर्जा ज्ञात कीजिये।
उत्तर:
माना कि एक पिण्ड घूर्णन गति कर रहा है। इस पिण्ड के कणों के द्रव्यमान क्रमशः m1, m2, m3, ….., mn तथा इनकी घूर्णन अक्ष से लम्बवत् दूरी r1, r2, r3, ….., rn है। तथा इनके रेखीय वेग क्रमशः v1, v2, v3, …., vn हैं तथा पिण्ड के प्रत्येक कण का कोणीय वेग ω है।
गति के कारण m1 द्रव्यमान वाले कण की गतिज ऊर्जा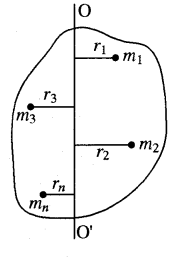
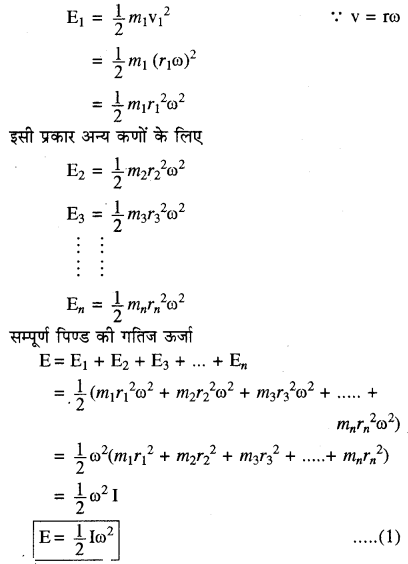
जहाँ I = m1r12 + m1r22 + m3r32 +….. + mnrn2 पिण्ड का जड़त्व आघूर्ण है। यदि ω = 1 रेडियन/सेकण्ड हो तो
I= 2E …………….(2)
अर्थात् किसी नियत अक्ष के सापेक्ष पिण्ड के जड़त्व आघूर्ण का मान संख्यात्मक रूप से घूर्णन गतिज ऊर्जा के दुगुने के बराबर होता है। जबकि पिण्ड का कोणीय वेग एकांक हो।
प्रश्न 11.
नत तल पर लोटनी गति कर रही वस्तु के त्वरण के लिये सूत्र व्युत्पन्न कीजिये।
उत्तर:
माना कि किसी नत तल का झुकाव कोण θ तथा ऊँचाई h है। कोई पिण्ड नत तल के शीर्ष बिन्दु से लुढ़कना शुरू करता है। पिण्ड का द्रव्यमान m तथा उसकी त्रिज्या R है।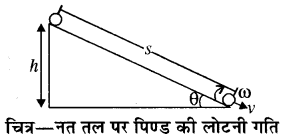
जब पिण्ड नत तल पर लुढ़केगा तो उसकी गति स्थानान्तरीय तथा घूर्णी दोनों प्रकार की होगी अतः पिण्ड की कुल गतिज ऊर्जा।
E = Et + Er
E = (frac{1}{2}) mv2 + (frac{1}{2}) Iω2 ………….(1)
जब पिण्ड नत तल के शीर्ष पर होगा तो उसकी कुल ऊर्जा केवल स्थितिज ऊर्जा होगी तथा इसका मान mgh के बराबर होता है। जब पिण्ड लुढ़कना प्रारम्भ करेगा तब स्थितिज ऊर्जा गतिज ऊर्जा में परिवर्तित होगी। अतः ऊर्जा संरक्षण के नियम से
mgh = (frac{1}{2}) mv2 + (frac{1}{2}) Iω2 ………(2)
यदि पिण्ड की घूर्णन त्रिज्या K हो तो
I = mK2 तथा ω = (frac{v}{R})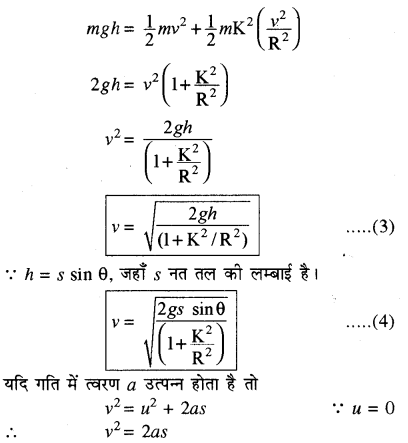
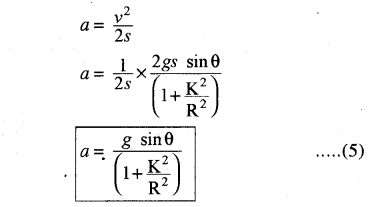
प्रश्न 12.
जड़त्व आघूर्ण का भौतिक महत्व क्या है?
उत्तर:
जिस प्रकार रेखीय गति में वस्तु का द्रव्यमान m वस्तु के जड़त्व की माप करता है उसी प्रकार घूर्णन गति में जड़त्व आघूर्ण I वस्तु के घूर्णन जड़त्व की माप करता है। इस प्रकार पिण्ड का द्रव्यमान (m) इसके जड़त्व का गुणांक का मापक है जबकि जड़त्व आघूर्ण (I) पिण्ड के घूर्णन जड़त्व को गुणांक का मापन करता है।
रेखीय गति में किसी वस्तु का द्रव्यमान अधिक होने पर उसकी स्थिति में परिवर्तन करने के लिये अधिक बल लगाना पड़ता है। उसी प्रकार घूर्णन गति में वस्तु का जड़त्व आघूर्ण जितना अधिक होता है, उसकी कोणीय स्थिति में परिवर्तन करने के लिये उतने ही अधिक बल आघूर्ण लगाने की आवश्यकता होती है। यही जड़त्व आघूर्ण का भौतिक महत्व है। इस प्रकार यह स्पष्ट है कि जो कार्य द्रव्यमान (m) रेखीय गति में करता है, घूर्णन गति में वही कार्य जड़त्व आघूर्ण (I) करता है।
रेखीय गति के सूत्रों में जहाँ द्रव्यमान (m) आता है, वहीं कोणीय गति के सूत्रों में जड़त्व आघूर्ण (I) आता है। जड़त्व आघूर्ण का हमारे जीवन में बहुत ही महत्त्व होता है। मोटरकार, स्कूटर, रिक्शा, बच्चों के खिलौने, साइकिल आदि में पहिये का जड़त्व आघूर्ण बढ़ाने के लिए पहियों का अधिकांश द्रव्यमान उनके रिमों पर स्थित होता है तथा रिम एवं पहिये की अक्ष का सम्बन्ध तानों की सहायता से कर दिया जाता है। पहिये के जड़त्व आघूर्ण अधिक होने के कारण ही जब हम साइकिल के पैडिल पर पैर चलाना बन्द कर देते। हैं तो कुछ दूरी तक अथवा कुछ समय तक साइकिल के पहिये घूमते रहते हैं।
प्रश्न 13.
किसी पतली छड़ को उसकी लम्बाई के लम्बवत् किनारे पर स्थित अक्ष के सापेक्ष जड़त्व आघूर्ण ज्ञात कीजिये।
उत्तर:
छड़ का AB अक्ष के सापेक्ष जड़त्व आघूर्ण ज्ञात करना। है। समान्तर अक्षों की प्रमेय से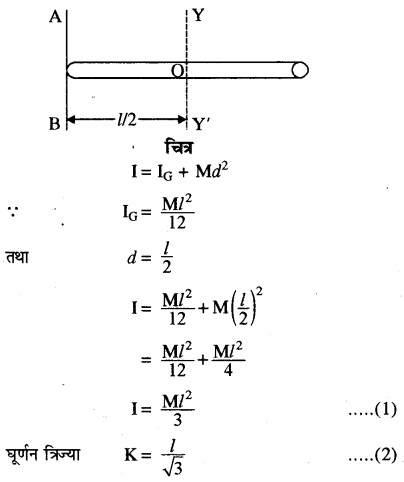
प्रश्न 14.
नततल पर लोटनी गति कर रही किसी वस्तु की तली के निचले सिरे पर कुल गतिज ऊर्जा का सूत्र लिखिये।
उत्तर:
माना कोई पिण्ड चित्रानुसार किसी झुके हुए तल पर बिना फिसले लुढ़क रहा है। तल की धरातल से ऊँचाई h, झुकाव कोण θ तथा पिण्ड का द्रव्यमान M है।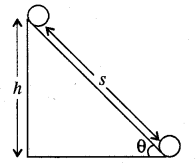
जब पिण्ड नीचे की ओर आता है तब इसकी स्थितिज ऊर्जा में कमी होती है तथा गतिज ऊर्जा में वृद्धि होती। है। लोटनी गति में पिण्ड की दो गतिज ऊर्जायें होती हैं-(i) रेखीय गतिज ऊर्जा (ii) घूर्णन गतिज ऊर्जा।
ऊर्जा संरक्षण के नियम से
स्थितिज ऊर्जा में कमी = गतिज ऊर्जा में वृद्धि
अर्थात् Mgh = (frac{1}{2}) Mv2 + (frac{1}{2}) Iω2 …………. (1)
अतः तली पर कुल गतिज ऊर्जा
K.E. = (frac{1}{2}) Mv2 + (frac{1}{2}) Iω2
प्रश्न 15.
कोणीय संवेग व कोणीय वेग में सम्बन्ध स्थापित कीजिये।
उत्तर:
माना कि कोई पिण्ड आघूर्ण अक्ष के परितः कोणीय वेग (ω) से घूर्णन गति कर रहा है। पिण्ड के सभी कणों के रेखीय वेग भिन्न-भिन्न तथा कोणीय वेग समान होगा। माना पिण्ड़ के कणों के द्रव्यमान m1, m2, m3, ….. mn हैं। इन घूर्णन अक्ष से लम्बवत् दूरियाँ क्रमशः r1, r2, r3, …..rn हैं तथा रेखीय वेग क्रमशः v1, v2, v3, ………., vn
m1 द्रव्यमान वाले कण का रेखीय संवेग
P1 = m1v1
P1 = m1r1ω ∵ v1 = r1ω
कोणीय संवेग L1 = r1P1
= r1 × m1r1ω ∵ P1 = m1r1ω
L1 = m1r12ω
इसी तरह से m2 द्रव्यमान वाले कण का कोणीय संवेग L2 = m2r22ω होगा।
इसी तरह से m3 द्रव्यमान वाले कण को कोणीय संवेग
L3 = m3r32ω
…………………..
………………….
Ln = mnrn2ω
वस्तु के समस्त कणों के द्रव्यमानों के संवेग के आघूर्गों का योग । सम्पूर्ण वस्तु के कोणीय संवेग के बराबर होता है। इसलिए पिण्ड का कोणीय संवेग
L = L1 + L2 + L3 + ….. + Ln
L = m1r12ω + m2r22ω + m3r32ω + ………… + mnrn2ω
L = ω(m1r12 + m2r22 + m3r32 + …………… + mnrn2)
L = Iω
जहाँ पर I = m1r12 + m<sub2r22 + m3r32 + …………… + mnrn2
जो कि पिण्ड का जड़त्व आघूर्ण है।
इस प्रकार किसी पिण्ड का किसी घूर्णन अक्ष के सापेक्ष कोणीय संवेग उसके उसी अक्ष के सापेक्ष जड़त्व आघूर्ण एवं उसके कोणीय वेग के गुणनफल के बराबर होता है।
RBSE Class 11 Physics Chapter 7 निबन्धात्मक प्रश्न
प्रश्न 1.
द्रव्यमान केन्द्र से क्या अभिप्राय है? दो कणों के निकाय के द्रव्यमान केन्द्र की स्थिति का व्यंजक प्राप्त कीजिये।
उत्तर:
किसी पिण्ड या निकाय का द्रव्यमान केन्द्र वह बिन्दु होता है। जहाँ पिण्ड का सम्पूर्ण द्रव्यमान केन्द्रित माना जा सकता है। स्पष्टतः बाह्य बल के प्रभाव में किसी निकाय की गति उसी बल के प्रभाव में द्रव्यमान केन्द्र की गति के तुल्य होती है। दूसरे शब्दों में, द्रव्यमान केन्द्र वह बिन्दु है जिसके परितः सभी कणों के द्रव्यमान तथा उनके स्थिति सदिशों के गुणनफल अर्थात् द्रव्यमान आधूर्गों का योग शून्य के बराबर होता है।
यदि किसी पिण्ड में स्थित कणों के द्रव्यमान m1, m2, m3, ….. mn, हों एवं इनकी द्रव्यमान केन्द्र (C) से दूरियाँ क्रमशः r1, r2, r3, ……rn, हों तो द्रव्यमान केन्द्र की परिभाषा के अनुसार
(m_{1} vec{r}_{1}+m_{2} vec{r}_{2}+m_{3} vec{r}_{3}+ldots . .+m_{n} vec{r}_{n}=0)
या (sum_{i=1}^{n} m_{i} vec{r}_{i}=0)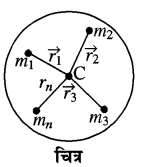
नियमित ज्यामिति आकार की वस्तुओं के लिए, यह वह बिन्दु होता है जिसके चारों ओर वस्तु सममित रूप में होती है तथा अनियमित आकार की वस्तुओं के लिए वह द्रव्यमान के वितरण पर निर्भर करेगा परन्तु निर्देश तंत्र पर निर्भर नहीं करेगा।
यदि कोई दृढ़ पिण्ड बाह्य बल के प्रभाव में गति कर रहा है तो उसकी गति का विश्लेषण द्रव्यमान केन्द्र बिन्दु पर उतना ही बल लगाता हुआ मानकर किया जा सकता है। गति के समय द्रव्यमान केन्द्र की स्थिति परिवर्तित नहीं होती।
द्रव्यमान केन्द्र की स्थिति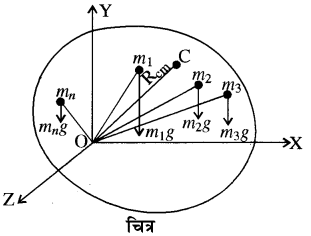
माना एक दृढ़ पिण्ड n कणों से मिलकर बना है जिसके द्रव्यमान क्रमशः m1, m2 व m3, हैं तथा एक निश्चित बिन्दु के सापेक्ष इनकी स्थितियाँ क्रमशः (overrightarrow{r_{1}}), (overrightarrow{r_{2}}) व (overrightarrow{r_{n}}) हैं। प्रत्येक कण पर गुरुत्वीय बल कार्य करता है जिसका मान उसके भार के तुल्य होता है। चित्र में इन बलों की दिशायें, यदि इनका विस्तार किया जाये तो पृथ्वी के केन्द्र से गुजरती हैं। यदि समस्त कणों के भार की बल रेखाओं को समान्तर माना जाये तो पिण्ड का कुल भार होगा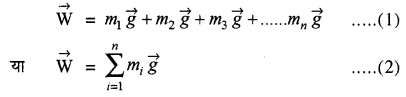
यदि इन कणों के भार को किसी बिन्दु विशेष (द्रव्यमान केन्द्र) पर कार्यरत माना जाये तो
समस्त भार का बिन्दु स्थिति RCM पर आघूर्ण = प्रत्येक कण के भार के आघूर्ण का योग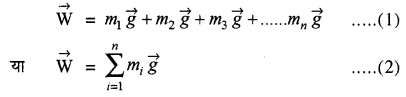
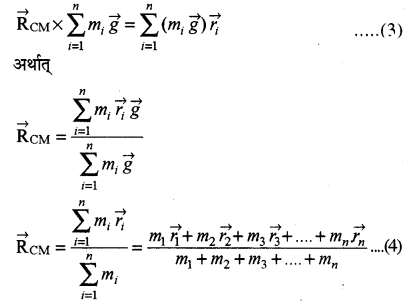
(overrightarrow{mathrm{R}}_{mathrm{CM}}) द्रव्यमान केन्द्र का स्थिति सदिश है। सममित पिण्डों के लिए द्रव्यमान केन्द्र व गुरुत्वीय केन्द्र बिन्दु सम्पाती होते हैं जबकि असममित पिण्डों में द्रव्यमान केन्द्र व द्रव्यमान केन्द्र की स्थिति भिन्न-भिन्न हो सकती है। गुरुत्वीय केन्द्र सदैव पिण्ड के अन्दर स्थित होता है परन्तु द्रव्यमान केन्द्र सदैव पिण्ड के अन्दर हो यह आवश्यक नहीं है।
माना द्रव्यमान केन्द्र के निर्देशांक (XCM, YCM, ZCM) हैं तथा कणों के निर्देशांक क्रमशः (x1, y1, z1), (x2, y2, z2), …….. व (xn, yn, zn ) हैं अतः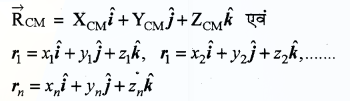

यदि संदर्भ बिन्दु की स्थिति (द्रव्यमान केन्द्र की स्थिति) निर्देशांक तंत्र के मूल बिन्दु पर स्थित हो तो उस बिन्दु पर समस्त कणों के द्रव्यमानों के आघूर्गों का योग शून्य होगा। अर्थात्
(sum_{i=1}^{n} m_{i} vec{r}_{i}=0) …………(9)
सतत द्रव्यमान वितरण की वस्तुओं या निकाय के लिये द्रव्यमान केन्द्र की स्थिति के मान उपरोक्त समीकरणों से ज्ञात नहीं किये जा सकते। सतत द्रव्यमान वितरण के पिण्डों में जैसे बेलन, मीटर स्केल, चकती इत्यादि कणों की संख्या का मान अत्यधिक होता है। ऐसी स्थिति में द्रव्यमान केन्द्र की स्थिति को ज्ञात करने के लिये एक चर राशि कैल्कुलस (One variable calculus) का उपयोग किया जाता है।
माना एक सतत द्रव्यमान का पिण्ड Δm1, Δm2) द्रव्यमान के n छोटे-छोटे भागों से मिलकर बना हुआ है। यदि पिण्ड का द्रव्यमान M हो तो।
M = Δm1 + Δm1 +…………Δmn …………….(10)
यदि i वे खण्ड के द्रव्यमान का मान Δmi एवं स्थिति (xi, yi, zi) हो तो ऐसी स्थिति में द्रव्यमान केन्द्र के निर्देशांक बिन्दुओं को निम्न प्रकार से व्यक्त कर सकते हैं
(mathbf{X}_{mathrm{CM}}=frac{sum_{i=1}^{n} Delta m_{i} x_{i}}{sum_{i=1}^{n} Delta m_{i}}) ……….(11)
द्विकण तंत्र द्रव्यमान केन्द्र
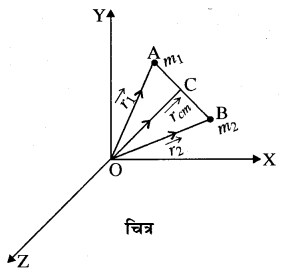
चित्र में दर्शाये अनुसार दो कण A तथा B हैं जिनके द्रव्यमान क्रमशः m1 तथा m2 हैं तथा निर्देश बिन्दु O से स्थिति सदिश (vec{r}_{1}) व (vec{r}_{2}) हैं, इन कणों का आपस में तथा बाह्य वातावरण से सम्बन्ध है।
माना कि प्रथम कण (A) पर द्वितीय कण (B) द्वारा लगने वाला आन्तरिक बल (overrightarrow{mathrm{F}}_{1}^{prime}) तथा बाह्य बल (overrightarrow{mathrm{F}_{1}^{prime prime}}) कार्यरत है तो कण m1 परे लगने वाला परिणामी बल
(overrightarrow{mathrm{F}}_{1}=overrightarrow{mathrm{F}}_{1}^{prime}+overrightarrow{mathrm{F}}_{1}^{prime prime})
न्यूटन के द्वितीय नियम से संवेग परिवर्तन की दर आरोपित बल के बराबर होती है।
(overrightarrow{mathrm{F}_{1}}=overrightarrow{mathrm{F}_{1}}^{prime}+overrightarrow{mathrm{F}_{1}^{prime prime}}=frac{d overrightarrow{mathrm{P}_{1}}}{d t}) ……………(1)
जहाँ A पर स्थित द्रव्यमान m1 के कण का संवेग (overrightarrow{mathrm{P}_{1}}) है। इसी प्रकार B पर स्थित द्रव्यमान m2 के कण पर बाह्य बल (overrightarrow{mathrm{F}}_{2}^{prime}) तथा दूसरे कण A द्वारा आन्तरिक बल (overrightarrow{mathrm{F}_{2}^{prime prime}}) लगा है तो द्वितीय कण पर कुल परिणामी बल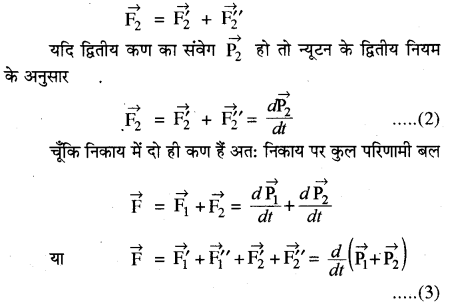
परन्तु न्यूटन के क्रिया-प्रतिक्रिया के तृतीय नियम के अनुसार
दोनों कणों के मध्य लगने वाले आन्तरिक बल परस्पर बराबर तथा विपरीत दिशा में कार्य करते हैं तथा इनका निकाय की गति में योगदान शून्य होगा अतः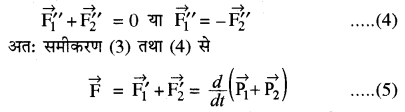
अतः दो कणों के निकाय पर कार्यरत परिणामी बल उन कणों पर लगने वाले बाह्य बलों के सदिश योग के बराबर होता है।

अतः समीकरण (7) से स्पष्ट है कि बाह्य बल (overrightarrow{mathrm{F}}) सम्पूर्ण पिण्ड के द्रव्यमान M पर एक नियत बिन्दु C पर लग रहा है, जिसको स्थिति सदिश (vec{r}_{c m}) है तथा यही बिन्दु दो कणों के निकाय का द्रव्यमान केन्द्र है, जिसे समीकरण (8) की सहायता से प्राप्त करते हैं। यदि द्रव्यमान केन्द्र मूल बिन्दु पर स्थित हो तो (vec{r}_{c m}) = 0 उस स्थिति में समीकरण (8) की सहायता से हम निम्न प्राप्त कर सकते हैं|
(m_{1} vec{r}_{1}+m_{2} vec{r}_{2}=0) …………..(9)
अर्थात् द्रव्यमान केन्द्र के परितः सभी द्रव्यमान आघूर्गों का सदिश योग शून्य होता है। समीकरण (9) से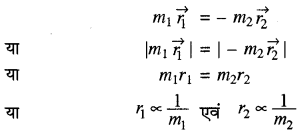
अर्थात् हम कह सकते हैं कि दो कणों के निकाय में कणों की। द्रव्यमान केन्द्र से दूरी उनके द्रव्यमानों के व्युत्क्रमानुपाती होती है। यदि m1 = m2 = ना हो तो समीकरण (8) से
(vec{r}_{c m}=frac{overrightarrow{r_{1}}+overrightarrow{r_{2}}}{2})
अर्थात् समान द्रव्यमान वाले कणों का द्रव्यमान केन्द्र उनके मध्य में स्थित होता है।
प्रश्न 2.
जड़त्व अधूर्ण प्रमेयों का कथन दीजिये तथा इनको सिद्ध भी कीजिये।
उत्तर:
लम्बवत् या समकोणिक अक्षों की प्रमेय
(Theorem of Perpendicular Axis)
किसी समतल पटल (Plane lamina) का इसके तल के लम्बवत् अक्ष के सापेक्ष जड़त्व-आघूर्ण इसके तल में स्थित दो पारस्परिक लम्बवत् अक्षों के सापेक्ष जड़त्व-आघूर्णो के योग के तुल्य होता है। जबकि अभीष्ट अक्ष दोनों लम्बवत् अक्षों के कटान बिन्दु से होकर गुजरती हैं।
यदि किसी समतल पटल का जड़त्व-आघूर्ण दो लम्बवत् अक्षों (OX व OY के सापेक्ष Ix तथा Iy हों और इनके कटान बिन्दु से गुजरने वाली अभिलम्बवंत् अक्ष (OZ) के सापेक्ष जड़त्व आघूर्ण Iz हो तो लम्बवत् अक्षों की प्रमेय से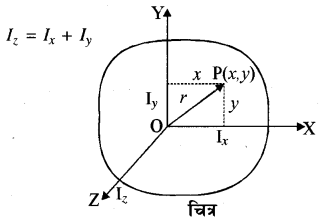
उपपत्ति (Proof)
चित्र के अनुसार माना OX तथा OY समतल पटल में दो लम्बवत् अक्ष हैं। OZ-अक्ष पटल के लम्बवत् है और बिन्दु O से न गुजरती है। बिन्दु P पर m द्रव्यमान का कण विद्यमान है। OX के सापेक्ष पटल का जड़त्व-आघूर्ण
Ix = Σmy2
इसी प्रकार OY अक्ष के सापेक्ष पटल का जड़त्व आघूर्ण
Iy = Σmx2
OZ के सापेक्ष पटल का जड़त्व आघूर्ण
Iz = Σmr2 = Σm(OP)2
= Σm (x2 + y2)
= Σmx2 + Σmy2
∴ Iz = Ix + Iy
प्रत्येक पिण्ड घूर्णन अक्ष के लम्बवत् अनेक समतल पटलों में विभाजित किया जा सकता है। अतः उपरोक्त प्रमेय सभी पिण्डों के लिये यथार्थ होती है।
समान्तर अक्षों की प्रमेय (Theorem of Parallel Axis)
किसी पिण्ड का किसी घूर्णन अक्ष के सापेक्ष जड़त्व आघूर्ण पिण्ड के गुरुत्व केन्द्र से गुजरने वाली समान्तर अक्ष के सापेक्ष पिण्ड का जड़त्व आघूर्ण तथा उसके द्रव्यमान और दोनों समान्तर अक्षों के मध्य लम्बवत् दूरी के वर्ग के गुणनफल के योग के तुल्य होता है।
यदि किसी समतल पटल का जड़त्व-अधूर्ण पटल के लम्बवत् अक्ष (CD) के सापेक्ष I हो तथा उसके गुरुत्व केन्द्र G से पारित समान्तर अक्ष (AB) के सापेक्ष IG हो, पटल का द्रव्यमान M तथा दोनों समान्तर अक्षों के बीच लम्बवत् दूरी d हो तो समान्तर अक्षों की प्रमेय से
I = IG + Md2 ………….(1)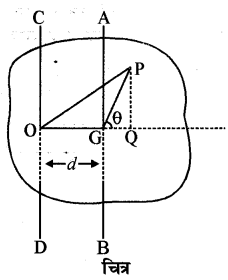
उपपत्ति (Proof)
चित्र के अनुसार माना m द्रव्यमान का कण बिन्दु P पर विद्यमान है जिसकी अक्ष CD से दूरी OP, अक्ष AB से दूरी GP हो तो
OP2 = OQ2 + QP2
(OG + GQ)2 + QP2 = OG2 + 20G . GQ + GQ2 + QP2
= OG2 + GP2 + 20G. GP cos θ ………….(2)
{GP2= GQ2 + QP2 तथा GQ = GP cos θ}
यहाँ θ OG व GP के मध्य बाह्य कोण है। G पटल का गुरुत्व केन्द्र है तथा O से घूर्णन अक्ष पारित होती है।
समी. (2) के दोनों पक्षों में m से गुणा करने पर
m.OP2 = m.OG2 + m. GP2 + 2m.OG.GP cos θ …………..(3)
यदि G से पारित अक्ष के सापेक्ष पटेल का जड़त्व आघूर्ण ; हो तो
IG = Σmr2 = Σm(GP)2
एवं O से पारित अक्ष के सापेक्ष पटल का जड़त्व आघूर्ण I हो तो ।
I = Σm(OP)2
समी. (३) को सभी कणों के लिये लिखने पर
Σm(OP)2 = Σm(OG)2 + Σm(GP) + Σ2m(OG).GP cos θ
या I = (OG)2 Σm + Σm(GP)2 + 2Σm(OG).(G Pcos θ)
= d2 Σm + IG + 2d Σm(GP) cos θ
क्योंकि OG = 4 नियत है।
परन्तु Σm(GP) cos θ = 0
क्योंकि AB गुरुत्व केन्द्र से होकर जाता है तथा गुरुत्व केन्द्र के प्रति कणों के द्रव्यमान आघूर्गों का योग शून्य होता है। अतः
I = IG + d2 Σm
= IG + Md2 (∵ M = Σm)
प्रश्न 3.
किसी चकती को उसके केन्द्र से पारित तल के लम्बवत् अक्ष के सापेक्ष जड़त्व आघूर्ण ज्ञात कीजिये।
उत्तर:
चकती के केन्द्र से गुजरने वाली तथा इसके तल के लम्बवत् अक्ष के सापेक्ष जड़त्व आघूर्ण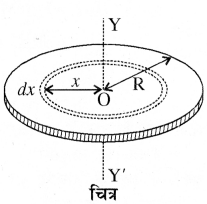
चित्र में दिखाये अनुसार M द्रव्यमान की एक समरूपी चकती की त्रिज्या R है और O इसका ज्यामिति केन्द्र है। हमें चकती का जड़त्व आघूर्ण YY’ अक्ष, जो कि चकती के केन्द्र से गुजरती है तथा इसके तल के लम्बवत् है, के सापेक्ष ज्ञात करना है।
एकांक क्षेत्रफल का द्रव्यमान = (frac{M}{pi R^{2}})
चकती को अनेक संकेन्द्रीय परिवर्ती त्रिज्या की वलयों से मिलकर बना हुआ मान सकते हैं। यहाँ पर हमने एक ऐसी वलर पर विचार किया है जिसकी त्रिज्या ५ तथा मोटाई dx है। इस वलय का द्रव्यमान
dm = चकती के एकांक क्षेत्रफल का द्रव्यमान × विचार की गई वलय का क्षेत्रफल
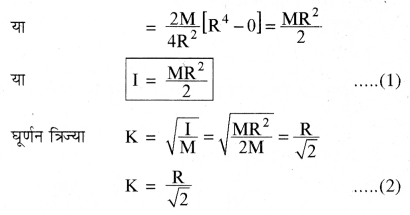
प्रश्न 4.
एक ठोस बेलन का उसकी लम्बाई के लम्बवत् एवं द्रव्यमान केन्द्र से गुजरने वाली अक्ष के सापेक्ष जड़त्व आघूर्ण ज्ञात कीजिये।
उत्तर:
ठोस बेलन का उसकी लम्बाई के लम्बवत् एवं द्रव्यमान-केन्द्र से गुजरने वाली अक्ष के सापेक्ष जड़त्व आघूर्ण (Moment of Inertia of Solid Cylinder about an Axis passing through its Centre of Mass and Perpendicular to it’s Length)
चित्रानुसार माना M, द्रव्यमान व R त्रिज्या तथा लम्बाई L का एक ठोस बेलन है। हमें जड़त्व आघूर्ण का मान बेलन की लम्बाई के लम्बवत् YY’ एवं द्रव्यमान केन्द्र O से गुजरने वाली अक्ष के सापेक्ष ज्ञात करना है।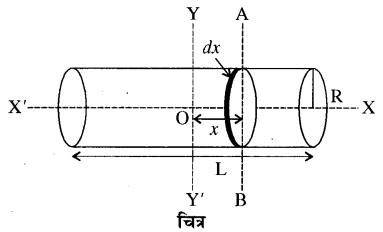
विचाराधीन चकती का आयतन = (πR2) dx
ठोस बेलन के एकांक आयतन का द्रव्यमान
= (frac{M}{pi R^{2} L})
अतः विचाराधीन चकती का द्रव्यमान
dm = (πR2) dx . (frac{mathbf{M}}{pi mathrm{R}^{2} mathrm{L}})
dm = (frac{M}{L}) dx
विचाराधीन चकती के द्रव्यमान-केन्द्र से गुजरती अक्ष AB चकती का एक व्यास होगी जिसके सापेक्ष चकती का जड़त्व आघूर्ण
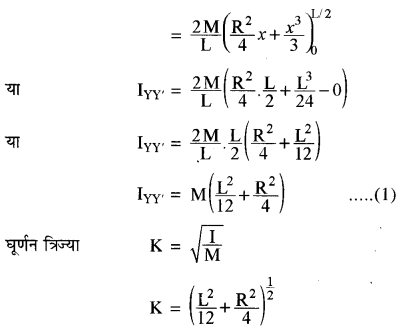
प्रश्न 5.
किसी ठोस गोले का इसके व्यास के सापेक्ष जड़त्व आघूर्ण ज्ञात कीजिये।
उत्तर:
ठोस गोले का जड़त्व आघूर्ण (Moment of Inertia of a Solid Sphere)
ठोस गोले का उसके व्यास के सापेक्ष जड़त्व आघूर्ण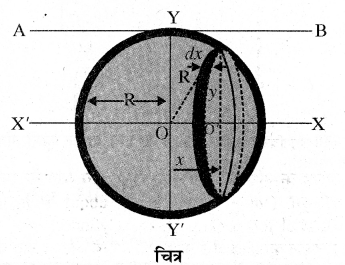
गोले को हम बहुत सी चकतियों से बना मान सकते हैं। जिनके पृष्ठ YY’ के समान्तर हैं तथा केन्द्र अक्ष XX’ पर स्थित है। इनमें से एक चकती का केन्द्र O’ है जिसकी त्रिज्या y है तथा O’ की गोले के केन्द्र O से x दूरी है। इस चकती की अनन्त सूक्ष्म मोटाई dx है।।
गोले का घनत्व (ρ) = (frac{mathrm{M}}{frac{4}{3} pi mathrm{R}^{3}})
चकती का आयतन = πy2dx एवं चकती का द्रव्यमान (dm) = πy2 dx ρ
अतः चकती के तल के लम्बवत् एवं केन्द्र से गुजरने वाली अक्ष XX’ के सापेक्ष जड़त्व आघूर्ण
dI = (frac{1}{2} d m y^{2})
= (frac{1}{2}left(pi y^{2} d x cdot rhoright) y^{2})
= (frac{1}{2}) πy4ρdx
= (frac{1}{2}) π(R2 – x2)2 ρdx (∵ y2 = R2 – x2)
सम्पूर्ण गोले का जड़त्व आघूर्ण XX’ अक्ष के सापेक्ष, उन सभी | चकतियों के जड़त्व आघूर्णो के योग के बराबर होगा जो x = – R से x = + R के मध्य स्थित हैं। अतः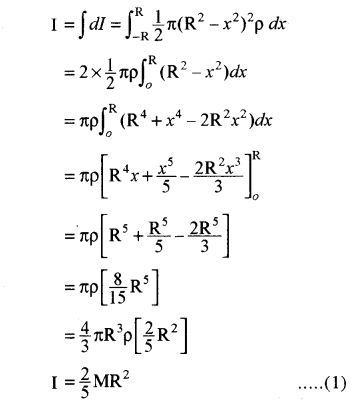
यही गोले का उसके व्यास के सापेक्ष जड़त्व आघूर्ण को व्यंजक है।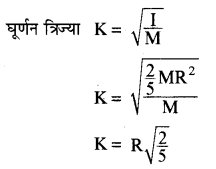
प्रश्न 6.
आयताकार छड़ का उसके द्रव्यमान केन्द्र से गुजरने वाली व छड़ की लम्बाई के लम्बवत् अक्ष के सापेक्ष जड़त्व आघूर्ण के सूत्र को व्युत्पन्न कीजिये।
उत्तर:
आयताकार अनुप्रस्थ काट की ठोस छड़ (Solid Rod of Rectangular Cross-section)
लम्बाई के लम्बवत् तथा द्रव्यमान केन्द्र से गुजरने वाली अक्ष के सापेक्ष जड़त्व आघूर्ण (Moment of Inertia about an Axis passing through the Centre of Mass and Perpendicular to its Length)-चित्र (II) में एक आयताकार ठोस छड़ प्रदर्शित की गई है, जिसकी लम्बाई L, चौड़ाई B, मोटाई d एवं द्रव्यमान M है। इस छड़ को अनेक पतले आयताकार पटलों से मिलकर बना हुआ मान सकते हैं। सम्पूर्ण आयताकार छड़ का जड़त्व आघूर्ण इन सभी आयताकार पटलों (Rectangular lamina) के जड़त्व आघूर्णो के योग के बराबर होगा। माना प्रत्येक आयताकार पटल का द्रव्यमान m है। आयताकार पटल के चित्र (I) के अनुसार अक्ष YY’ के समान्तर x दूरी पर dx चौड़ी एक आयताकार पट्टी (strip) है। यदि पटल का एकांक क्षेत्रफल का द्रव्यमान ० हो, तो पट्टी का द्रव्यमान Bdo होगा। अतः YY’ अक्ष के सापेक्ष पट्टी का जड़त्व आघूर्ण = Bdxσx2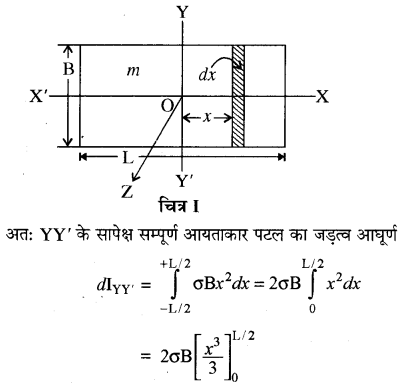
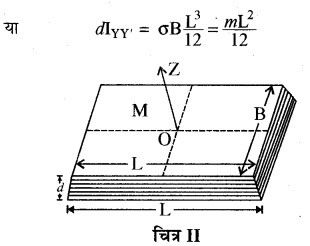
यहाँ m = σBL आयताकार पटल का द्रव्यमान है।
इसी प्रकार XX’ अक्ष के सापेक्ष पटल का जड़त्व आघूर्ण
dIXX’ = (frac{m mathrm{B}^{2}}{12})
dIYY’‘ व dIXX’ एक ही तल में दो परस्पर लम्बवत् अक्षों के सापेक्ष जड़त्व आघूर्ण हैं। चित्र (I) में इन अक्षों के प्रतिच्छेदन बिन्दु से लम्बवत् अक्ष OZ के सापेक्ष जड़त्व आघूर्ण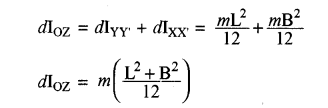
यह एक आयताकार पटल का Z अक्ष के सापेक्ष जड़त्व आघूर्ण है। इस प्रकार के सब आयताकार पटलों का Z अक्ष के सापेक्ष जड़त्व आघूर्गों का योग ही आयताकार छड़ का जड़त्व आघूर्ण होगा। अतः चित्र (II) में आयताकार छड़ की लम्बाई के लम्बवत् व केन्द्र से गुजरने वाली OZ अक्ष के सापेक्ष जड़त्व आघूर्ण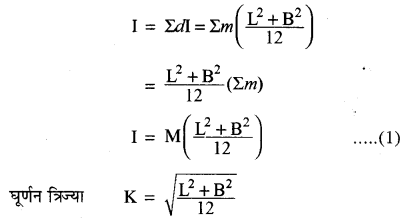
प्रश्न 7.
किसी खोखले गोले को उसके व्यास के सापेक्ष जड़त्व आघूर्ण ज्ञात कीजिये।
उत्तर:
खोखले गोले का उसके व्यास के सापेक्ष जड़त्व आघूर्ण
माना एक खोखले गोले का द्रव्यमान M, घनत्व ρ, भीतरी त्रिज्या R2 तथा बाहरी त्रिज्या R1 है (चित्र)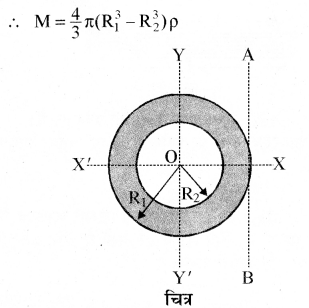
खोखले गोले का जड़त्व आघूर्ण (I)
= R1 त्रिज्या के ठोस गोले का जडत्व आघूर्ण
– R2 त्रिज्या के ठोस गोले का जड़त्व आघूर्ण
I = (frac{2}{5})(M1R12 – M2R22)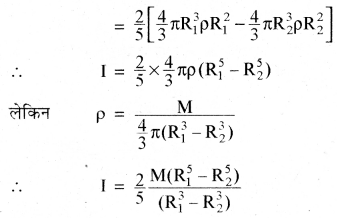
विशेष अवस्था
जब R2 = 0 तथा R1 = R
I = (frac{2}{5})MR2
(b) स्पर्श रेखा के सापेक्ष जड़त्व आघूर्ण
समान्तर अक्ष प्रमेय से
I = IG + Md2
IAB = Iyy’ + MRI12
IAB = (frac{2}{5} mathrm{M}left[frac{left(mathrm{R}_{1}^{5}-mathrm{R}_{2}^{5}right)}{left(mathrm{R}_{1}^{3}-mathrm{R}_{2}^{3}right)}right]+mathrm{MR}_{1}^{2})
प्रश्न 8.
सिद्ध कीजिये कि एक पिण्ड की, जो घूर्णन गति में है, गतिज ऊर्जा (frac{1}{2}) Iω2 है।
उत्तर:
घूर्णन गतिज ऊर्जा
(Kinetic Energy of Rotation)
चित्र में दिखाये अनुसार एक दृढ़ वस्तु PQ अक्ष के सापेक्ष घूर्णन कर रही है। इस वस्तु के कणों के द्रव्यमान m1, m2, m3, ….. mn, की घूर्णन अक्ष से दूरी क्रमशः r1, r2, r3,……rn, आदि हैं, यहाँ पर वस्तु घूर्णन अक्ष के सापेक्ष एक नियत कोणीय वेग ω से घूर्णन कर रही है और इनके प्रत्येक कण का रेखीय वेग क्रमशः v1 = r1ω, v2 = r2ω, v3 = r3ω …… आदि हैं।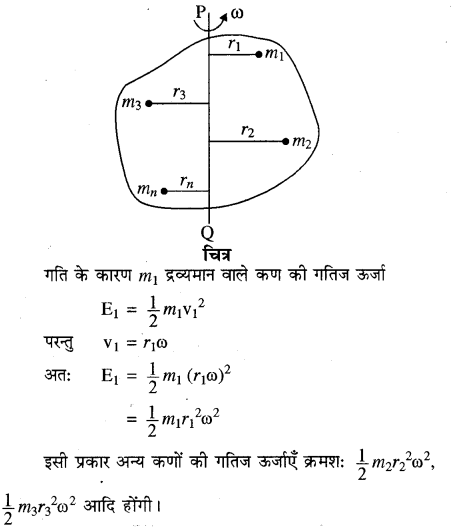
चूँकि गतिज ऊर्जा एक अदिश राशि है, अतः सम्पूर्ण दृढ़ वस्तु । की गतिज ऊर्जा (E), कणों की गतिज ऊर्जाओं का योग होगा अर्थात्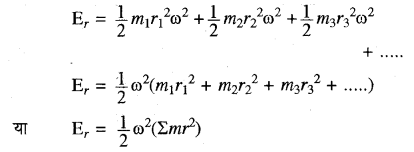
परन्तु Σmr2, दृढ़ वस्तु का घूर्णन अक्ष के सापेक्ष जड़त्व आघूर्ण (I) है अतः
Er = (frac{1}{2})ω2I …………..(1)
यही घूर्णन करती हुई दृढ़ वस्तु की घूर्णन गतिज ऊर्जा है। यदि ω = 1 रेडियन/से. हो तो
Er = (frac{1}{2}) × (1)2I = (frac{1}{2})I
या I = 2Er
अतः किसी अक्ष के परितः एकांक कोणीय वेग से घूमने वाले दृढ़ वस्तु का जड़त्व आघूर्ण, दी हुई अक्ष के परितः वस्तु की घूर्णन गतिज ऊर्जा के दुगुने के बराबर होता है।
यदि कोई वस्तु घूर्णन गति के साथ-साथ रेखीय गति भी करती हो, तो वस्तु की कुल गतिज ऊर्जा, घूर्णन गतिज ऊर्जा एवं रेखीय गतिज ऊर्जा के योग के बराबर होगी।
ETotal = KE. = (frac{1}{2})Iω2 + (frac{1}{2})mv2
प्रश्न 9.
एक समान पतली छड़ का जड़त्व आघूर्ण उसके एक सिरे से गुजरते तथा लम्बाई के लम्बवत् अक्ष के सापेक्ष ज्ञात करो।
उत्तर:
लम्बाई के लम्बवत् किनारे से गुजरने वाली छड़ के सापेक्ष जड़त्व आघूर्ण (Moment of Inertia about an Axis Perpendicular to the Length and passing through One Edge)- जब एकसमान पतली छड़ की लम्बाई के लम्बवत् P बिन्दु से गुजरने वाले अक्ष के सापेक्ष जड़त्व आघूर्ण I’ हो, तो समान्तर अक्ष प्रमेय से
प्रश्न 10.
नंते तल पर लोटनी गति कर रही वस्तु के लिये वेग व त्वरण के लिये सूत्र का मान व्युत्पन्न कीजिये।
उत्तर:
नत तल पर लोटनी गति
(Rolling Motion on an Inclined Plane)
माना कोई पिण्ड चित्रानुसार किसी झुके हुए तल पर बिना फिसले लुढ़क रहा है। तल की धरातल से ऊँचाई h, झुकाव कोण θ तथा पिण्ड का द्रव्यमान M है।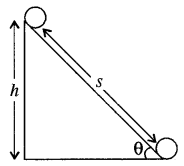
जब पिण्ड नीचे की ओर आता है तब इसकी स्थितिज ऊर्जा में कमी होती है तथा गतिज ऊर्जा में वृद्धि होती है। लोटनी गति में पिण्ड की दो गतिज ऊर्जायें होती हैं-(i) रेखीय गतिज ऊर्जा (ii) घूर्णन गतिज ऊर्जा।
ऊर्जा संरक्षण के नियम से
स्थितिज ऊर्जा में कमी = गतिज ऊर्जा में वृद्धि
अर्थात् Mgh = (frac{1}{2})Mv2+ (frac{1}{2})Iω2 ………. (1)
यहाँ पर y तल के नीचे पहुँचने पर उसके द्रव्यमान केन्द्र का रेखीय वेग है तथा ω उसका द्रव्यमान केन्द्र के परितः कोणीय वेग है।
I = MK2 तथा V = Rω
जहाँ K घूर्णन त्रिज्या है।
∴ Mgh =(frac{1}{2})Mv2 + (frac{1}{2})MK2 (left(frac{mathrm{v}^{2}}{mathrm{R}^{2}}right)) ………….. (2)
यह नत तल पर लुढ़कती हुई वस्तु के त्वरण का व्यंजक है। किसी नत तल पर लुढ़कने वाली वस्तु में उत्पन्न त्वरण का मान (left(frac{mathrm{K}^{2}}{mathrm{R}^{2}}right)) पर निर्भर करता है।
(left(frac{mathrm{K}^{2}}{mathrm{R}^{2}}right)) का मान कम होने पर त्वरण a का मान अधिक होगा। नत तल के निम्नतम बिन्दु तक पहुँचने में लगा समय गति के द्वितीय समीकरण से ज्ञात कर सकते हैं।
(i) जब भिन्न-भिन्न आकृति के पिण्ड एक साथ शीर्ष बिन्दु से लुढ़काये जायें तो धरातल पर पहुँचने में लगा समय (left(frac{mathrm{K}^{2}}{mathrm{R}^{2}}right)) पर निर्भर करता है। समीकरण (6) से स्पष्ट है कि (left(frac{mathrm{K}^{2}}{mathrm{R}^{2}}right)) का मान अधिक होने पर t का मान भी अधिक प्राप्त होगा।
लुढ़कने वाली विभिन्न वस्तुओं के लिए (left(frac{mathrm{K}^{2}}{mathrm{R}^{2}}right)) के मान
स्पष्ट है कि यदि वलय, चकती, बेलन, गोले की एक साथ लोटनी गति कराई जाए तो नत तल के नीचे ठोस गोला सबसे पहले वे वलय सबसे बाद में पहुँचेगी। चकती एवं ठोस बेलन का (left(frac{mathrm{K}^{2}}{mathrm{R}^{2}}right)) का मान समान होने के कारण साथ-साथ पहुँचेंगे।
नत तल पर फिसलते हुए पिण्ड की स्थिति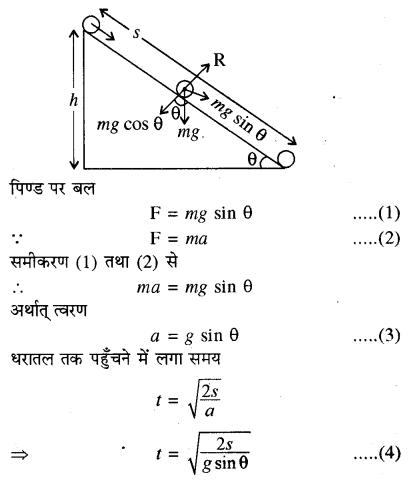
RBSE Class 11 Physics Chapter 7 आंकिक प्रश्न
प्रश्न 1.
दो कण जिनके वेग क्रमशः ((hat{i}+hat{j}-hat{k})) तथा ((3 hat{i}-2 hat{j}+hat{k})) cm s-1 हैं, द्विकण निकाय का निर्माण करते हैं। यदि कणों के द्रव्यमान क्रमशः 5 g व 2 g हों तो निकाय के द्रव्यमान केन्द्र का वेग क्या होगा?
हल:
(vec{v}_{c m}=frac{m_{1} vec{v}_{1}+m_{2} vec{v}_{2}}{m_{1}+m_{2}})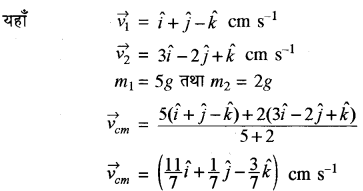
प्रश्न 2.
एक पहिया जो विरामावस्था में है, 3.0 rad s-2 के कोणीय त्वरण के अन्तर्गत 2.0 s तक घूमता है। इस समयान्तराल में पहिया कितना कोणीय वेग अर्जित करेगा तथा उसमें कितना विस्थापन होगा?
हल:
दिया है- ω0 = 0 rad s-1
α = 3.0 rad s-2
t = 2.0 s
ω = ?, θ = ?
ω = ω0 + αt
ω = 0 + 3 x× 2 = 6.0 rad s-1
θ = ω0t + (frac{1}{2}) αt2
θ = 0 + (frac{1}{2}) × 3 × (2)2 = 6.0 rad.
प्रश्न 3.
एक कार जो विराम अवस्था में है, 40rad s-2 के कोणीय त्वरण से त्वरित होती है। यह कितने समय में 800 चक्कर/ मिनट का कोणीय वेग प्राप्त करेगी?
हल:
दिया है- ω0 = 0 rad s-1
α = 40 rad s-2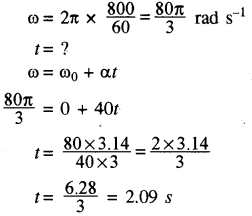
प्रश्न 4.
एक समबाहु त्रिभुज के शीर्षों पर रखे गये तीन कणों का द्रव्यमान केन्द्र ज्ञात कीजिये, कणों के द्रव्यमान क्रमशः 100 g, 150 g एवं 200 g हैं। त्रिभुज की प्रत्येक भुजा की लम्बाई 0.5m है।
हल:
माना कि त्रिभुज का एक शीर्ष (O) मूल बिन्दु पर स्थित है तथा एक भुजा X-अक्ष के अनुदिश है। माना द्रव्यमान केन्द्र के निर्देशांक xCM तथा yCM हैं।
∴ निकाय के द्रव्यमान केन्द्र के निर्देशांक
(x_{mathrm{CM}}=frac{m_{1} x_{1}+m_{2} x_{2}+m_{3} x_{3}}{m_{1}+m_{2}+m_{3}})
m1 = 100 ग्राम, m2 = 150 ग्राम, m3 = 200 ग्राम
x1 = 0 मी., x2 = 0.5 मी., x3 = 0.25 मी.
उपरोक्त निकाय के द्रव्यमान केन्द्र के निर्देशांक (left(frac{5}{18}, frac{1}{3 sqrt{3}}right)) मी. होंगे।
प्रश्न 5.
एक घूर्णन करते हुए पिण्ड में 4 rad s-2 का कोणीय त्वरण उत्पन्न करने के लिये 2.0 × 10-4 N m का बल आघूर्ण लगाना पड़ता है। पिण्ड का जड़त्व आघूर्ण क्या है?
हल:
दिया है- θ = 4 rad s-2
τ = 2 × 10-4 Nm
I = ?
τ = Iα
I = (frac{tau}{alpha}=frac{2 times 10^{-4}}{4})
I = 0.5 × 10-4 kg m2
प्रश्न 6.
एक द्विपरमाणुक अणु (diatomic molecule) में दो परमाणुओं का द्रव्यमान m1 तथा m2 है। इन परमाणुओं के बीच अचर दूरी α मीटर है। निकाय का जड़त्व आघूर्ण, निकाय के गुरुत्वीय केन्द्र तथा परमाणुओं को जोड़ने वाली रेखा के लम्बवत् गुजरने वाले अक्ष के सापेक्ष ज्ञात करो।
हल: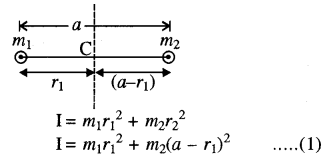

प्रश्न 7.
एक वृत्ताकार चकती जिसकी त्रिज्या 0.5 m एवं द्रव्यमान 25 kg है, अपनी धुरी पर 120 चक्कर/मिनट की रफ्तार से घूर्णन करती है। चकती का जड़त्व आघूर्ण एवं घूर्णन की गतिज ऊर्जा का परिकलन कीजिये।
हल:
दिया है- R= 0.5 m
M = 25 kg
n = (frac{120}{60}) चक्कर/s = 2 चक्कर/s
I = ? Er = ?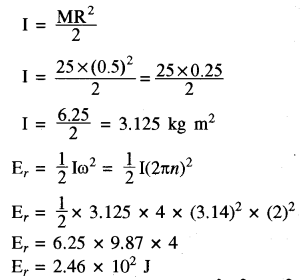
प्रश्न 8.
एक M द्रव्यमान तथा l लम्बाई की पतली छड़ का जड़त्व आघूर्ण उसकी लम्बाई के लम्बवत् तथा एक सिरे से l/4 बिन्दु से गुजरने वाली अक्ष के सापेक्ष क्या होगा?
हल: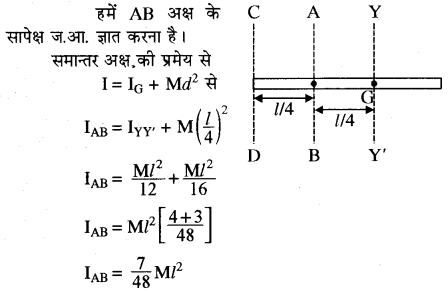
प्रश्न 9.
गोलीय पृथ्वी का अपनी स्वयं की अक्ष के सापेक्ष घूर्णन के कोणीय संवेग की गणना कीजिये। (पृथ्वी का द्रव्यमान 6 × 1024 kg तथा त्रिज्या 6.4 × 106 m)
हल:
J = Iω
पृथ्वी की स्वयं की अक्ष व्यास होती है।
प्रश्न 10.
एक खोखले गोले का द्रव्यमान 1 kg है एवं उसकी भीतरी व बाहरी त्रिज्या क्रमशः 0.1 m एवं 0.2 m है। गोले के व्यास के सापेक्ष जड़त्व आघूर्ण एवं परिभ्रमण त्रिज्या ज्ञात करो।
हल:
दिया है- M= 1 kg
R1 = 0.2 m
R2= 0.1 m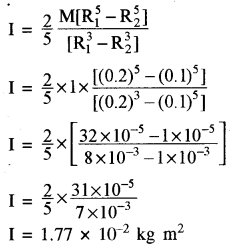
K = (sqrt{frac{mathrm{I}}{mathrm{M}}}=sqrt{frac{1.77 times 10^{-2}}{1}})
K = 1.33 × 10-1 = 0.133 m
प्रश्न 11.
1 kg द्रव्यमान की एक गेंद 20 m s-1 के वेग से क्षैतिज तल पर गति करते हुए एक तल पर जो क्षैतिज से 30° का कोण बनाता है, के पैंदे पर पहुँचती है। यदि घर्षण नगण्य हो तो गेंद कितनी ऊध्र्वाधर ऊँचाई पर चढ़ सकेगी?
हल:
दिया है- M = 1 kg
v = 20 m s-1
θ = 30°
h = ?, g = 10 m s-2
यांत्रिक ऊर्जा संरक्षण नियम से
कुल गतिज ऊर्जा में कमी = कुल गतिज ऊर्जा में वृद्धि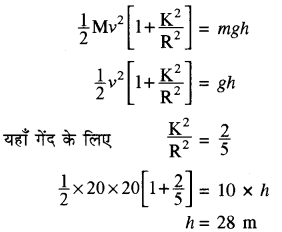
प्रश्न 12.
तीन पिण्ड एक वलय, एक ठोस बेलन और एक गोला, एक नततल पर बिना फिसले लोटनी गति करते हैं। वे विरामावस्था से गति शुरू करते हैं। सभी पिण्डों की त्रिज्यायें बराबर हैं। कौनसा पिण्ड नत तल के आधार पर सबसे अधिक वेग से पहुँचता है?
हल: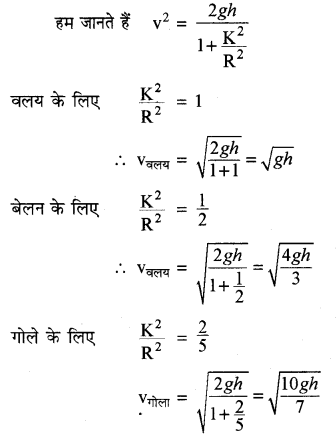
प्राप्त परिणामों से यह स्पष्ट होता है कि नत तल की तली में पहुँचने पर तीनों पिण्डों में गोले के द्रव्यमान केन्द्र का वेग सबसे अधिक और वलय के द्रव्यमान केन्द्र का वेग सबसे कम होगा।
यदि पिण्डों के द्रव्यमान समान हों तो नत तल की तली में पहुँचने पर गोले पिण्ड की गतिज ऊर्जा सबसे अधिक होगी।
प्रश्न 13.
यदि द्रव्यमान नियत रखकर किसी घूर्णन करती हुई चकती की त्रिज्या अचानक आधी कर दी जाये तो उसका नवीन कोणीय वेग का मान कितना होगा?
हलं:
कोणीय संवेग संरक्षण नियम से,
I’ω’ = Iω
(frac{mathrm{MR}^{prime 2}}{2}) ω’ = (frac{mathrm{MR}^{2}}{2}) ω
R2ω’ = R2ω / परन्तु R’ = (frac{mathrm{R}}{2})
(frac{mathrm{R}^{2}}{4})ω’ = R2ω
ω’ = 4ω
अर्थात् नवीन कोणीय वेग चार गुना हो जायेगा।
प्रश्न 14.
एक पिण्ड का कोणीय वेग बिना उस पर बल आघूर्ण लगाये 1 चक्कर/से. से 16 चक्कर/से. हो जाता है। दोनों अवस्थाओं में घूर्णन त्रिज्याओं का अनुपात क्या होगा?
हल:
बल आघूर्ण की अनुपस्थिति में पिण्ड का कोणीय संवेग संरक्षित रहता है। अतः
I’ω’ = Iω
n’ = 16 चक्कर/s
n = 1 चक्कर/s
MK’2.(2πn’) = MK2.2πn
K’2n’ = K2n
(frac{mathrm{K}}{mathrm{K}^{prime}}=sqrt{frac{n^{prime}}{n}}=sqrt{frac{16}{1}})
(frac{mathrm{K}}{mathrm{K}^{prime}}=frac{4}{1})
अर्थात् K : K’= 4: 1
प्रश्न 15.
M व N दो पहिये एक ही धुरी पर हैं। M का जड़त्व आघूर्ण 6 kg m’ तथा 600 घूर्णन/मिनट से घूर्णन कर रहा है तथा N स्थिर है। एक क्लच द्वारा दोनों को जोड़ने पर संयुक्त रूप से 400 घूर्णन/मिनट करते हैं तो N के जड़त्व आघूर्ण का मान ज्ञात कीजिये।
हल:
दिया है- IM = 6 kg m2
All Chapter RBSE Solutions For Class 12 Physics Hindi Medium
—————————————————————————–
All Subject RBSE Solutions For Class 11 Hindi Medium
*************************************************
————————————————————
All Chapter RBSE Solutions For Class 11 physics Hindi Medium
All Subject RBSE Solutions For Class 11 Hindi Medium
Remark:
हम उम्मीद रखते है कि यह RBSE Class 11 physics Solutions in Hindi आपकी स्टडी में उपयोगी साबित हुए होंगे | अगर आप लोगो को इससे रिलेटेड कोई भी किसी भी प्रकार का डॉउट हो तो कमेंट बॉक्स में कमेंट करके पूंछ सकते है |
यदि इन solutions से आपको हेल्प मिली हो तो आप इन्हे अपने Classmates & Friends के साथ शेयर कर सकते है और HindiLearning.in को सोशल मीडिया में शेयर कर सकते है, जिससे हमारा मोटिवेशन बढ़ेगा और हम आप लोगो के लिए ऐसे ही और मैटेरियल अपलोड कर पाएंगे |
आपके भविष्य के लिए शुभकामनाएं!!