हेलो स्टूडेंट्स, यहां हमने राजस्थान बोर्ड कक्षा 11वीं की भौतिक विज्ञान सॉल्यूशंस को दिया हैं। यह solutions स्टूडेंट के परीक्षा में बहुत सहायक होंगे | Student RBSE solutions for Class 11 Physics Chapter 14 गैसों का अगुणित सिद्धान्त pdf Download करे| RBSE solutions for Class 11 Physics Chapter 14 गैसों का अगुणित सिद्धान्त notes will help you.
Table of Contents
Rajasthan Board RBSE Class 11 Physics Chapter 14 गैसों का अगुणित सिद्धान्त
RBSE Class 11 Physics Chapter 14 पाठ्य पुस्तक के प्रश्न एवं उत्तर
RBSE Class 11 Physics Chapter 14 अतिलघूत्तरात्मक प्रश्न
प्रश्न 1.
किसी ताप T पर आदर्श गैस के लिये वर्ग माध्य मूल वेग क्या होता है?
उत्तर:
vrms = (sqrt{frac{3 mathrm{RT}}{mathrm{M}}}) यहाँ M = गैस का अणु भार, T= गैस का परम ताप व R = सार्वत्रिक नियतांक है।
प्रश्न 2.
गैस नियतांक (R) का मात्रक क्या होता है?
उत्तर:
Jmol-1K-1
प्रश्न 3.
किसी गैस का परम ताप 16 गुना बढ़ा दिया जाये तो उसका वर्ग माध्य मूल वेग कितना गुना हो जायेगा?
उत्तर:
4 गुना
प्रश्न 4,
वाण्डरवाल समीकरण लिखिये।
उत्तर:
(P + (frac{a}{V^{2}})) (V – b) = nRT
यहाँ P V व T क्रमशः वास्तविक गैस के दाब, आयतन व ताप हैं जबकि n अणुओं की संख्या घनत्व, R सार्वत्रिक गैस नियतांक तथा a व b वाण्डरवाल नियतांक है।
प्रश्न 5.
गैस के अणुगति सिद्धान्त के अनुसार परम शून्य ताप पर गैस के अणु की चाल क्या होती है?
उत्तर:
शून्य
प्रश्न 6.
स्वतंत्रता की कोटि (f) व रुद्धोष्म निष्पत्ति (γ) में सम्बन्ध बताइये।
उत्तर:
γ = (1 + (frac{2}{f})) यहाँ f स्वतत्रंता की कोटि है।
प्रश्न 7.
एक वायुयान आकाश में उड़ रहा है तो उसकी स्वतंत्रता की कोटि क्या होगी?
उत्तर:
3
प्रश्न 8.
किसी द्विपरमाणुक गैस के लिए CP का मान बताइये।
उत्तर:
(frac{7}{2}) R यहाँ R = सार्वत्रिक गैस नियतांक है।
प्रश्न 9.
गैस के अणुगति सिद्धान्त द्वारा दाब का सूत्र लिखिये।
उत्तर:
P = (frac{1}{3} frac{m n overline{v}^{2}}{V}) जहाँ m अणु का द्वव्यमान, n अणुओं की संख्या घनत्व, (overline{v}^{2}) माध्य वर्ग वेग, V गैस का आयतन तथा ρ गैस का घनत्व है।
प्रश्न 10.
आवोगाद्रो संख्या का मान क्या होता है?
उत्तर:
6.023 × 1023
RBSE Class 11 Physics Chapter 14 लघूत्तरात्मक प्रश्न
प्रश्न 1.
गैसों के अणुगति सिद्धान्त के अभिगृहितों की व्याख्या कीजिये।
उत्तर:
गैसों की अणुगति सिद्धान्त की परिकल्पनायें
गैसों के विभिन्न भौतिक गुणों की गैसों के अणुगति सिद्धान्त से व्याख्या करने के लिये निम्न परिकल्पनायें ली जाती हैं
- एक गैस के सभी अणु आकार तथा द्रव्यमान में समान और वे पूर्णतः प्रत्यास्थ होते हैं।
- गैस के अणुओं का आयतन गैस के आयतन की तुलना में नगण्य होता है।
- गैस के अणुओं का वेग (0, -∞ ) के बीच होता है तथा वे हर सम्भव वेग से हर सम्भव दिशा में गतिमान रहते हैं। गैस का ताप अणुओं की गतिज ऊर्जा के समानुपाती होता है।
- गैस के अणुओं के बीच टक्कर पूर्णतया प्रत्यास्थ होती है। तथा अणुओं की टक्कर में लगा समय नगण्य होता है। इसकी कोटि 10-8 सेकण्ड होती है।
- टक्कर से पूर्व सीधी रेखा में अणु द्वारा तय की गई दूरी को मुक्त पथ कहते हैं तथा निश्चित टक्करों के बाद माध्य तय की गई दूरी को औसत मुक्त पथ कहते हैं।
- अणुओं के बीच कोई आकर्षण तथा प्रतिकर्षण बल कार्य नहीं करता है।
- गैस के अणुओं पर गुरुत्वाकर्षण बल प्रभावी नहीं होता है। क्योंकि अणुओं का द्रव्यमान सूक्ष्म तथा वेग अधिक होता है।
- गैस का घनत्व पूरी गैस के सभी भागों में लगभग समान होता है।
- जब गैस के गतिशील अणु बर्तन की दीवार से टकराते हैं तो उनके संवेग में परिवर्तन होता है और वे परिवर्तन संवेग को पात्र की। दीवारों को स्थानान्तरित करते हैं, जिसके कारण गैस बर्तन की दीवार पर दबाव उत्पन्न करती है।
सीमाबद्धता
- अणुगति सिद्धान्त की परिकल्पनाओं में माना गया है कि गैस के अणुओं के बीच में आकर्षण या प्रतिकर्षण बल नहीं लगता है। परन्तु जब गैस के दो अणु एक-दूसरे के अत्यन्त समीप आते हैं तब उनके बीच प्रतिकर्षण बल लगने लगता है जिससे उनकी चाल तथा गति की दिशा बदल जाती है।
- गैस का दाब अधिक होता है तब गैस के अणुओं का आयतन जिस बर्तन में गैस है उसके मुकाबले में गैस के अणुओं का आयतन नगण्य नहीं माना जा सकता है।
- गैसों के अणुओं में आकर्षण बल भी होता है, जिसके कारण बर्तन की दीवार पर लगने वाला दाब आकर्षण न होने के मुकाबले कुम् दाब लगता है।
- गैस के अणु सिद्धान्त में माना गया है कि गैस के अणुओं का वेग (0, – ∞) तक होता है, जबकि कोई कण प्रकाश के वेग से अधिक वेग से गति नहीं कर सकता है।
प्रश्न 2.
गैस के अणुगति सिद्धान्त के अभिगृहितों के अनुसार गैस के भौतिक गुणों की विवेचना कीजिये।
उत्तर:
1. यदि गैस से भरे दो पात्रों को आपस में किसी पाइप के द्वारा जोड़ दिया जाये तो दोनों पात्रों में गैसों का घनत्व एकसमान हो जायेगा-अणुगति सिद्धान्त की अभिकल्पनाओं के आधार पर गैसों के अणुओं के मध्य दूरी बहुत अधिक होती है और इस कारण अणु ठोसों एवं द्रवों की तुलना में बहुत दूर-दूर होते हैं । अर्थात् गैसों का घनत्व ठोसों एवं द्रवों की तुलना में बहुत कम होता है। जब किसी गैस को दबाया जाता है तो गैस के अणु दबाव के प्रभाव में उन स्थानों में जाने। की कोशिश करते हैं जो रिक्त हैं। अतः यदि गैस से भरे दो पात्रों को आपस में किसी पाइप के द्वारा जोड़ दिया जाये तो दोनों पात्रों में गैसों का प्रवाह तब तक होता रहेगा जब तक दोनों पात्रों में गैसों का घनत्व एकसमान न हो जाए।
2. गैस के पात्र के किसी कोने में रखे इत्र की खुशबू का तुरंत पूरे पात्र में फैल जाना- अणुगति सिद्धान्त की अभिकल्पनाओं में माना गया है कि गैस के अणुओं के मध्य कोई भी आकर्षण बल नहीं है, अर्थात् इन अणुओं की कोई स्थितिज ऊर्जा नहीं है एवं सम्पूर्ण ऊर्जा गतिज ऊर्जा ही है। इस कारण अणुओं को जहाँ भी रिक्त स्थान मिलता है, वहीं जाने का प्रयास करते हैं। इस प्रकार इत्र की खुशबू पूरे पात्र में फैल जाती है।
3. नियत ताप पर किसी गैस का आयतन आधा कर दिया जाये तो दाब दुगुना हो जायेगा-गैस के अणु लगातार गतिमान हैं। ये अणु आपस में भी टकराते हैं और पात्र की दीवारों से भी टकराते हैं। पात्र की दीवार से टकराने पर अणुओं के संवेग में परिवर्तन होता है और इसके फलस्वरूप पात्र की दीवारों पर एक बल कार्यरत होता है। इकाई क्षेत्रफल पर कार्य करने वाले इसी बल को दाब कहते हैं। नियत ताप पर किसी गैस का आयतन जब आधा कर दिया जाये तो पात्र की दीवारों पर प्रति सेकण्ड टकराने वाले अणुओं की संख्या भी दुगुनी हो जायेगी। इस कारण पात्र की दीवारों पर कार्य करने वाला दाब दुगुना हो जायेगा।
4. नियत आयतन पर किसी गैस का ताप बढ़ा दिया जाये तो। गैस का दाब भी बढ़ जायेगा-यदि नियत आयतन के किसी पात्र में भरी हुई किसी गैस का ताप बढ़ाया जाये तो सम्पूर्ण ऊष्मा गैस के अणुओं की गतिज ऊर्जा में परिवर्तित हो जायेगी। (गैस के अणुओं के मातक विज्ञान (कक्षा-II) मध्ये कोई भी आकर्षण बल नहीं है, अतः इन अणुओं की कोई स्थितिज ऊर्जा नहीं है)। अर्थात् अणुओं की चाल बढ़ जाएगी। इससे पात्र की दीवारों पर प्रति सेकण्ड टकराने वाले अणुओं की संख्या में वृद्धि हो जायेगी और गैस का दाब बढ़ जायेगा।
5. किसी पात्र को आयतन व ताप नियत रखते हुए गैस की मात्रा दुगनी कर दी जाए तो गैस का दाब भी दुगुना हो जायेगा-किसी गैस में अणुओं की संख्या गैस की मात्रा के समानुपाती है। गैस की मात्रा दुगुनी करने पर अणुओं की संख्या भी दुगुनी हो जाएगी। इसके फलस्वरूप गैस का दाब भी दुगुना हो जायेगा।
प्रश्न 3.
गैस के अणुगति सिद्धान्त के अनुसार ताप की व्याख्या कीजिये
उत्तर:
जब पदार्थ को ऊष्मा देते हैं तब दी गई ऊष्मा पदार्थ के अणुओं में वितरित हो जाती है जिसे प्राप्त कर पदार्थ के अणु अंपनी सामान्य स्थिति के इर्द-गिर्द ज्यादा आयाम से सरल आवर्त गति करने लगते हैं। पदार्थ के द्रव या गैस होने पर अणुओं के कम्पन का आयाम बढ़ने के साथ रेखीय और चक्रण गतियाँ भी बढ़ जाती हैं और बढ़ी हुई कुल गतिज ऊर्जा दी हुई ऊष्मा के बराबर होती है। इस तरह पदार्थ को दी गई ऊष्मा पदार्थ के अणुओं की कुल गतिज ऊर्जा के रूप में बदल जाती है और पदार्थ की निश्चित मात्रा के ताप में वृद्धि दी गयी ऊष्मा वृद्धि के समानुपाती होती है।
इसलिये पदार्थ की निश्चित मात्रा को दी गयी ऊष्मा ∝ ताप में वृद्धि या पदार्थ की निश्चित मात्रा के अणुओं की कुल गतिज ऊर्जा में वृद्धि ∝ पदार्थ के ताप में वृद्धि हम जानते हैं कि 0 K पर पदार्थ के अणुओं की कुल गतिज ऊर्जा शून्य होती है। यदि पदार्थ की निश्चित मात्रा में T K पर अणु की कुल गतिज ऊर्जा E हो तब
E ∝ T
प्रश्न 4.
वास्तविक गैसों के लिये वाण्डरवाल गैस समीकरण की व्याख्या कीजिये।
उत्तर:
अन्तराण्विक अन्योन्य क्रिया- आदर्श गैस में अणुओं के मध्य किसी प्रकार के आकर्षण बल या प्रतिकर्षण बल नहीं होते हैं। जबकि वास्तविक गैसों में अणुओं के मध्य अन्तराण्विक बल होते हैं, जिन्हें वान्डरवाल बल भी कहते हैं। उच्च ताप व निम्न दाब पर इनके प्रभाव को नगण्य माना जा सकता है। परन्तु निम्न ताप उच्च दाब पर इनका प्रभाव नगण्य नहीं होता है। इस कारण गैस का वास्तविक दाब प्रेक्षित दाब से अधिक होगा। इसे निम्न प्रकार समझाया जा सकता है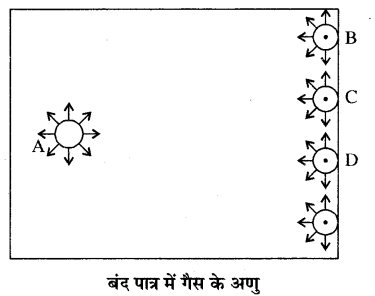
माना कि किसी बंद पात्र में गैस के n अणु भरे हैं। जो अणु पात्र में पूर्ण रूप से अन्दर हैं उन पर चारों ओर से अणुओं द्वारा समान रूप से आकर्षण बल लगेगा, इस कारण ऐसे अणुओं पर परिणामी अन्तराण्विक बल शून्य होगा। परन्तु वे अणु जो कि दीवार के समीप हैं, इन पर परिणामी अन्तराण्विक बल शून्य नहीं होगा परन्तु अन्दर की ओर कार्य करेगा। इस अन्दर की ओर खिंचाव के कारण दीवार से टकराते समय इन अणुओं के संवेग में कुछ कमी आ जाती है। इस कारण अणु दीवार पर उतना बल नहीं लगा पाते जितना कि वे अन्तराण्विक बलों की अनुपस्थिति में कर पाते। इस कमी को निम्न प्रकार से समझाया जा सकता है
n = पात्र में कुल अणुओं की संख्या
n1 = दीवार से टकराने वाले अणुओं की संख्या
n2 = दीवार से टकराने वाले अणुओं को भीतर खींचने वाले
अणुओं की संख्या
इस कारण दाब में कमी Pin
Pin ∝ n1
Pin ∝ n2
परन्तु
n1 ∝ n
n2 ∝ n
∴ Pin ∝ n2
n ∝ (frac{1}{V})
∴ Pin ∝ (frac{1}{mathrm{V}^{2}})
या Pin = (frac{a}{V^{2}})
यहाँ पर वान्डरवाल नियतांक है। इस कारणं गैस का वास्तविक दाब
P’ = (P + Pin)
= (left(P+frac{a}{V^{2}}right))
अतः एक ग्राम अणु भार के गैस का वास्तविक गैस समीकरण होगा
P’V’ = RT
(left(P+frac{a}{V^{2}}right)) (V – b) = RT
इसे वान्डरवाल गैस समीकरण भी कहते हैं।
गैस के n मोल का समीकरण निम्न होगा
(left(mathrm{P}+frac{a n^{2}}{mathrm{V}^{2}}right)) (V – nb) = nRT
प्रश्न 5.
स्वतंत्रता की कोटि से क्या अभिप्राय है?
उत्तर:
कोई कण या अणु या परमाणु जितनी दिशाओं में स्वतंत्रतापूर्वक गति कर सकता है, दिशाओं की उसे संख्या को कण की स्वतंत्रता कोटि कहते हैं।
उदाहरण के लिए, किसी छड़ में पिरोया हुआ छल्ला केवल छड़ की लम्बाई के अनुदिश ही चलने को स्वतंत्र है, अतः छल्ले की स्वतंत्रता कोटि एक होगी। इसी प्रकार कैरमबोर्ड पर चलने वाली गोटियाँ केवल उसकी लम्बाई व चौड़ाई तल में चल सकती हैं। अतः स्वतंत्रता कोटि दो होगी। आकाश में उड़ने वाले गुब्बारे की स्वतंत्रता कोटि तीन होगी क्योंकि वह तीनों (x, y व z) दिशाओं में उड़ने को स्वतंत्र है।
इसके अतिरिक्त किसी निकाय की सम्पूर्ण अवस्था या उसकी स्थिति तथा विन्यास को प्रदर्शित करने के लिए जितने स्वतंत्र निर्देशांकों या चरों की आवश्यकता होती है, उनकी संख्या को स्वतंत्रता कोटि कहते हैं।
स्वतंत्रता की कोटियाँ तीन प्रकार की होती हैं
(a) स्थानान्तरण की स्वतंत्रता की कोटियाँ
(b) घूर्णन की स्वतंत्रता की कोटियाँ
(c) कम्पन की स्वतंत्रता की कोटियाँ
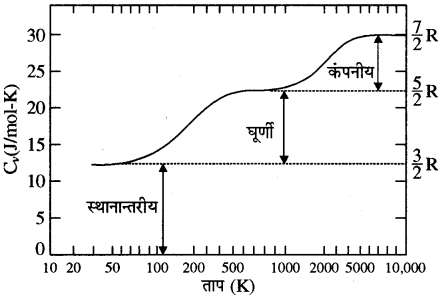
(a) स्थानान्तरण की स्वतंत्रता की कोटियाँ (Degrees of Freedom Translation Motion)- स्थानान्तरण की स्वतंत्रता की कोटियाँ अणु की स्थानान्तरीय या रेखीय गति के कारण उत्पन्न होती हैं। इनकी अधिकतम तीन होती हैं। ये सामान्य ताप पर उपस्थित होती हैं।
(b) घूर्णन की स्वतंत्रता की कोटियाँ (Degrees of Freedom of Rotation Motion)- घूर्णन की स्वतंत्रता की कोटि अणु के द्रव्यमान केन्द्र से पारित अक्ष के सापेक्ष घूर्णन गति के कारण होती है। इनकी संख्या अणु की संरचना पर निर्भर करती है। यह सामान्य ताप पर उपस्थित रहती हैं।
(c) कम्पन की स्वतंत्रता की कोटियाँ (Degrees of Freedom of Vibrational Motion)- कम्पन की स्वतंत्रता की कोटि अणुओं के कम्पनों के कारण होती है। इनकी संख्या भी अणु की संरचना पर निर्भर करती है। ये साधारणतया सामान्य ताप पर उपस्थित न होकर उच्च ताप पर उपस्थित होती हैं। इसमें प्रत्येक कम्पन तरीके के लिए कम्पन की स्वतंत्रता की कोटि दो होती हैं। इसमें से एक स्थितिज ऊर्जा व एक गतिज ऊर्जा के संगत।
माना N कणों से निर्मित एक निकाय में कणों के मध्य में स्वतन्त्र सम्बन्ध हो, तो निकाय की स्वतन्त्रता की कोटियाँ होंगी
f = 3N – k
प्रश्न 6.
गैस के अणुगति सिद्धान्त के अनुसार बॉयल के नियम की व्याख्या कीजिये।
उत्तर:
बॉयल का नियम (Boyle’s Law)
अणु गति सिद्धान्त के अनुसार दाब का समीकरण
P = (frac{1}{3} frac{m n overline{mathrm{C}}_{r m s}^{2}}{mathbf{V}}) ………… (1)
m = एक अणु का द्रव्यमान
n = अणुओं की संख्या
V = आयतन अणुओं की औसत गतिज ऊर्जा
(frac{1}{2} frac{m n overline{mathrm{C}}_{r m s}^{2}}{mathbf{V}}) ∝ T
∴ PV ∝ T
स्थिर ताप पर PV = नियतांक
अर्थात् नियत गैस की मात्रा का नियत ताप पर गैस दाब व आयतन का गुणा स्थिर रहता है।
प्रश्न 7.
ऊर्जा के सम विभाजन नियम पर टिप्पणी लिखिये।
उत्तर:
इस नियम को सर्वप्रथम मेक्सवेल ने गैसों के गत्यात्मक सिद्धान्त के आधार पर प्रतिपादित किया।
हम जानते हैं कि जब दो गैसें जो भिन्न-भिन्न ताप पर हैं, मिश्रित की जाती हैं तो उनके अणुओं की टक्करें होती हैं तथा गैस के अणुओं की ऊर्जाओं में अन्तर घटता जाता है जब तक दोनों गैसों की माध्य गतिज ऊर्जा समान नहीं हो जाती गतिज ऊर्जाएँ समान हो जाने पर ताप समान हो जाते हैं। यह अवस्था तापीय साम्य की अवस्था कहलाती है। इसे ही मैक्सवेल का ऊर्जा समविभाजन का नियम कहते हैं।
13.6 के समीकरण (1) को देखें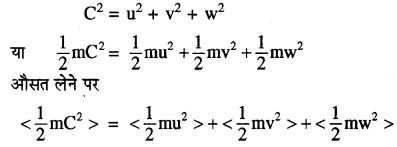
(frac{3}{2}) kT = KEx + KEy + KEz [गतिज ऊर्जा के सभी घटक समान हैं]
(frac{3}{2}) kT = 3<KE>औसत
<KE>औसत = (frac{1}{2}) kT
प्रति स्वतंत्रता कोटि के लिये बोल्ट्जमान ने इसी समविभाजन नियम को स्वातंत्र्य कोटि के रूप में निम्न प्रकार प्रतिपादित किया
“तापीय साम्य में किसी गतिकीय निकाय की कुल ऊर्जा उसकी समस्त स्वातंत्र्य कोटियों में समान रूप से वितरित होती है और इसका मान (frac{1}{2}) kT होता है।”
यदि किसी अणु की स्वतंत्रता कोटियाँ f हों तो उसकी ताप T पर कुल माध्य ऊर्जा होगी
(fleft(frac{1}{2} k Tright)=frac{1}{2} f k T)
एक ग्राम मोल गैस के अणुओं की कुल ऊर्जा
(mathrm{E}=mathrm{U}=mathrm{N}_{mathrm{A}} mathrm{f}left(frac{1}{2} mathrm{kT}right)=frac{1}{2} mathrm{f} mathrm{N}_{mathrm{A}} mathrm{kT})
चूँकि NAk = R
∴ E = U = (frac{1}{2})f RT
n मोल गैस के अणुओं की कुल ऊर्जा E = U = (frac{1}{2}) fn RT
प्रश्न 8.
एक-परमाणुक, द्वि-परमाणुक व बहु-परमाणुक गैस के लिये CP, CV व γ के मान ज्ञात कीजिये।
उत्तर:
पिछले अध्याय में हम पढ़ चुके हैं कि किसी भी गैस के m द्रव्यमान के ताप में ΔT परिवर्तन के लिए यदि ΔQ ऊष्मा दी जाए तो। विशिष्ट ऊष्मा C को निम्न सूत्र से ज्ञात किया जा सकता है
C = (frac{Delta Q}{m times Delta T})
भिन्न-भिन्न इकाई पद्धतियों में विशिष्ट ऊष्मा के मात्रक अलगअलग प्राप्त होते हैं।
C.G.S. पद्धति में विशिष्ट ऊष्मा का मात्रक erg gm-1 C°, M.K.S. पद्धति में विशिष्ट ऊष्मा का मात्रक Jkg-1 C° एवं मिश्रित पद्धतियों में विशिष्ट ऊष्मा के अन्य मात्रक J mole-1C°, calorie g-1C°, K calorie kg-1C° आदि प्राप्त होते हैं।
जल की विशिष्ट ऊष्मा (भिन्न-भिन्न मात्रक पद्धतियों में)
1 calorie g-1C°
1 k calorie kg-1C°
18 calorie mole-1C°
4200 J kg-1C°
75.6 J mole-1 °C-1
0.075 J mole-1C°
4.2 Jg-1C°
गैसों की विशिष्ट ऊष्मा को मान शून्य से अनन्त तक कुछ भी हो सकता है। यह मान इस बात पर निर्भर करेगा कि गैस को ऊष्मा कैसे दी गई।
रुद्धोष्म प्रक्रम में विशिष्ट ऊष्मा- किसी गैस को बिना ऊष्मा दिए यदि संपीडित किया जाए तो ताप में वृद्धि (AT धनात्मक) हो जाती है, तब
Cरुद्धोष्म = (frac{Delta Q}{m times Delta T}=frac{0}{m times Delta T}=0)
स्थिर आयतन पर मोलर विशिष्ट ऊष्मा (Cv)- स्थिर आयतन पर किसी गैस की एक मोल मात्रा का ताप 1°C या 1 K बढ़ाने के लिए दी गई ऊष्मा को स्थिर आयतन की मोलर विशिष्ट ऊष्मा (Cv) कहते हैं।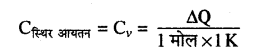
स्थिर आयतन पर मोलर विशिष्ट ऊष्मा (Cv)- स्थिर आयतन पर किसी गैस की एक मोल मात्रा का ताप 1°C या 1 K बढ़ाने के लिए दी गई ऊष्मा को स्थिर आयतन की मोलर विशिष्ट ऊष्मा (C) कहते हैं।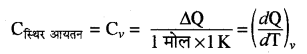
स्थिर दाब पर मोलर विशिष्ट ऊष्मा (Cp)- स्थिर दाब पर किसी गैस की एक मोल मात्रा का ताप 1°C या 1K बढ़ाने के लिए। दी गई ऊष्मा को स्थिर दाब की मोलर विशिष्ट ऊष्मा (Cp) कहते हैं।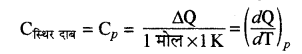
स्थिर आयतन पर ग्राम विशिष्ट ऊष्मा (cv)- स्थिर आयतन पर | किसी गैस की एक ग्राम मात्रा का ताप 1°C या 1 K बढ़ाने के लिए दी गई ऊष्मा को स्थिर आयतन की ग्राम विशिष्ट ऊष्मा (cv) कहते हैं। (cv = cv/M)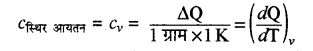
स्थिर दाबे पर ग्राम विशिष्ट ऊष्मा (cp)- स्थिर दाब पर किसी गैस की एक ग्राम मात्रा का ताप 1°C या 1 K बढ़ाने के लिए। दी गई ऊष्मा को स्थिर दाब की ग्राम विशिष्ट ऊष्मा (cp) कहते हैं। (cp = Cp/M)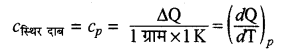
पिछले अध्याय में हम पढ़ चुके हैं कि Cp का मान.Cv से। अधिक होता है। (इसी प्रकार cp का मान भी cv से अधिक होता है)। मोलर विशिष्ट ऊष्माओं Cp तथा Cv का अन्तर सार्वत्रिक गैस नियतांक (R) कहलाता है। अतः Cp – Cv = R होता है तथा इस सम्बन्ध को मेयर का सम्बन्ध कहते हैं।
मोलर विशिष्ट ऊष्माओं Cp तथा Cv का अनुपात (γ) कहलाता है। अतः Cp/Cv = γ होता है।
गैसों की मोलर विशिष्ट ऊष्माओं (Cp तथा Cv) को स्वतंत्रता कोटियों से सम्बन्ध (f)- प्रत्येक गैस के एक अणु की एक स्वतंत्रता कोटि की ऊर्जा kT/2 होती है। अतः एक मोल गैस के अणुओं की (f) स्वतंत्रता कोटियों के लिए ऊर्जा होगी
U = N × f × (frac{1}{2}) kT
(यहाँ k = बोल्ट्जमान नियतांक)
(एक मोल गैस में अणुओं की संख्या आवोगाद्रो नियतांक NA के समान होती है)। .
प्रश्न 9.
किसी गैस के कणों के माध्य मुक्त पथ की व्याख्या कीजिये।
उत्तर:
गैसों के अणुगति सिद्धान्त के अनुसार किसी गैस के अणु हर सम्भव वेग से हर सम्भव दिशा में निरन्तर गति करते रहते हैं। इस गति के समय वे बर्तन की दीवारों से तथा आपस में टकराते रहते हैं जिससे उनके वेग, परिमाण और दिशा परिवर्तित होते रहते हैं। चूंकि टक्कर पूर्णतः प्रत्यास्थ होती है अतः दो क्रमागत टक्करों के मध्य अणु एक समान वेग से सरल रेखा में गति करते हैं। दो क्रमागत टक्करों के मध्य गैस के अणु द्वारा तय की गई दूरी मुक्त पथ कहलाती है। उत्तरोत्तर टक्करों के मध्य अणुओं द्वारा तय की गई दूरियाँ एकसमान नहीं होतीं।
अतः इन समस्त दूरियों का औसत निकालते हैं जिसे मुक्त माध्य पथ (Mean free path) कहते हैं।
मुक्त पथ λ =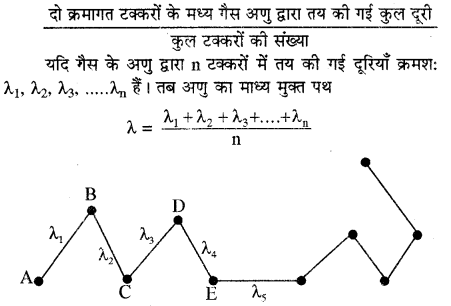
प्रश्न 10.
यदि किसी पात्र में अणुओं की संख्या का मान दुगुना कर दिया जाये तो उसके दाब में क्या परिवर्तन होगा?
उत्तर:
हम जानते हैं-PV = NkT, अर्थात् P ∝ N
अणुओं की संख्या दुगुनी करने पर दाब दुगुना हो जायेगा।
RBSE Class 11 Physics Chapter 14 निबंधात्मक प्रश्न
प्रश्न 1.
गैस के अणुगति सिद्धान्त के अभिगृहितों को लिखते हुए उससे बायल, चार्ल्स, गैलुसाक व डाल्टन के नियमों की व्याख्या कीजिये।
उत्तर:
गैसों की अणुगति सिद्धान्त की परिकल्पनायें
गैसों के विभिन्न भौतिक गुणों की गैसों के अणुगति सिद्धान्त से व्याख्या करने के लिये निम्न परिकल्पनायें ली जाती हैं
- एक गैस के सभी अणु आकार तथा द्रव्यमान में समान और वे | पूर्णतः प्रत्यास्थ होते हैं।
- गैस के अणुओं का आयतन गैस के आयतन की तुलना में नगण्य होता है।
- गैस के अणुओं का वेग (0, -∞ ) के बीच होता है तथा वे हर सम्भव वेग से हर सम्भव दिशा में गतिमान रहते हैं। गैस का ताप अणुओं की गतिज ऊर्जा के समानुपाती होता है।
- गैस के अणुओं के बीच टक्कर पूर्णतया प्रत्यास्थ होती है। तथा अणुओं की टक्कर में लगा समय नगण्य होता है। इसकी कोटि 10-8 सेकण्ड होती है।
- टक्कर से पूर्व सीधी रेखा में अणु द्वारा तय की गई दूरी को मुक्त पथ कहते हैं तथा निश्चित टक्करों के बाद माध्य तय की गई दूरी को औसत मुक्त पथ कहते हैं।
- अणुओं के बीच कोई आकर्षण तथा प्रतिकर्षण बल कार्य नहीं करता है।
- गैस के अणुओं पर गुरुत्वाकर्षण बल प्रभावी नहीं होता है। क्योंकि अणुओं का द्रव्यमान सूक्ष्म तथा वेग अधिक होता है।
- गैस का घनत्व पूरी गैस के सभी भागों में लगभग समान होता है।
- जब गैस के गतिशील अणु बर्तन की दीवार से टकराते हैं तो उनके संवेग में परिवर्तन होता है और वे परिवर्तन संवेग को पात्र की। दीवारों को स्थानान्तरित करते हैं, जिसके कारण गैस बर्तन की दीवार पर दबाव उत्पन्न करती है।
सीमाबद्धता
- अणुगति सिद्धान्त की परिकल्पनाओं में माना गया है कि गैस के अणुओं के बीच में आकर्षण या प्रतिकर्षण बल नहीं लगता है। परन्तु जब गैस के दो अणु एक-दूसरे के अत्यन्त समीप आते हैं तब उनके बीच प्रतिकर्षण बल लगने लगता है जिससे उनकी चाल | तथा गति की दिशा बदल जाती है।
- गैस का दाब अधिक होता है तब गैस के अणुओं का आयतन जिस बर्तन में गैस है उसके मुकाबले में गैस के अणुओं का आयतन नगण्य नहीं माना जा सकता है।
- गैसों के अणुओं में आकर्षण बल भी होता है, जिसके कारण बर्तन की दीवार पर लगने वाला दाब आकर्षण न होने के मुकाबले कुम् दाब लगता है।
- गैस के अणु सिद्धान्त में माना गया है कि गैस के अणुओं का वेग (0, – ∞) तक होता है, जबकि कोई कण प्रकाश के वेग से अधिक वेग से गति नहीं कर सकता है।
बॉयल का नियम (Boyle’s Law)
अणु गति सिद्धान्त के अनुसार दाब का समीकरण
P = (frac{1}{3} frac{m n overline{mathrm{C}}_{r m s}^{2}}{mathbf{V}}) ………… (1)
m = एक अणु का द्रव्यमान
n = अणुओं की संख्या
V = आयतन अणुओं की औसत गतिज ऊर्जा
(frac{1}{2} frac{m n overline{mathrm{C}}_{r m s}^{2}}{mathbf{V}}) ∝ T
∴ PV ∝ T
स्थिर ताप पर PV = नियतांक
अर्थात् नियत गैस की मात्रा का नियत ताप पर गैस दाब व आयतन का गुणा स्थिर रहता है।
चार्ल्स का नियम (Charles’s Law)
अणु गति सिद्धान्त से
यही चार्ल्स का नियम है।
अर्थात् किसी गैस की निश्चित मात्रा स्थिर दाब पर आयतन V ताप के समानुपाती होता है।
गैलुसाक को नियम (Gay-Lussac’s Law)
अणु गति सिद्धान्त से
यही गैलुसाक का नियम है अर्थात् किसी गैस की निश्चित मात्रा तथा स्थिर आयतन पर दाब ताप के समानुपाती होता है।
डॉल्टन के आंशिक दाब का नियम (Dalton’s Law of Partial Pressure)
इस नियम के अनुसार किसी पात्र में भरी अक्रियाशील गैसों के मिश्रण का कुल दाब प्रत्येक गैस के अलग-अलग आंशिक दाबों के योग के बराबर होता है, अर्थात्
P = P1 + P2 + P3 + P4 + ………………
यहाँ, P1, P2, P3,…… इत्यादि मिश्रित गैसों के आंशिक दाब हैं।
गैस के अणुगति सिद्धान्त के आधार पर समझने के लिए माना कि v आयतन के किसी पात्र में दो गैसों का मिश्रण है। गैस A के अणुओं की संख्या N1 व अणु द्रव्यमान m1 तथा गैस B के अणुओं की संख्या N2 व अणु द्रव्यमान m2 है। A तथा B गैस के अणुओं के वर्ग माध्य मूल वेग क्रमशः (Crms)1 व (Crms)2 हों तो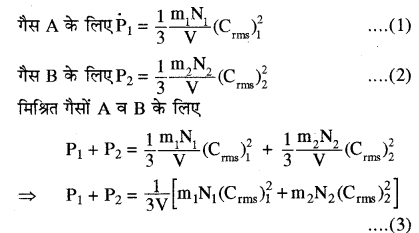
मिश्रित गैस के लिए नियत ताप पर दोनों गैसों के ताप समान हैं। अतः प्रति अणु माध्य गतिज ऊर्जायें समान होंगी।
अर्थात् (frac{1}{2} mathrm{m}_{1} overline{mathrm{C}_{1}^{2}}=frac{1}{2} mathrm{m}_{2} overline{mathrm{C}_{2}^{2}}=frac{1}{2} mathrm{m} overline{mathrm{C}^{2}})
समीकरण (3) से
P1 + P2 = (frac{1}{3 V}left(mathrm{N}_{1}+mathrm{N}_{2}right) mathrm{m} overline{mathrm{C}^{2}}) ………….. (4)
परन्तु (N1 + N2) मिश्रण में कुल अणुओं की संख्या है। गैस के मिश्रण के द्वारा उत्पन्न कुल दाब P होगा।
P = (frac{1}{3 V}left(mathrm{N}_{1}+mathrm{N}_{2}right) mathrm{m} overline{mathrm{C}^{2}}) …………. (5)
समीकरण (4) तथा (5) की तुलना करने पर
P = P1 + P2
यही डाल्टन का आंशिक दाब का नियम है।
दो से अधिक गैसों के मिश्रण के लिए
P = P1 + P2 + P3 + ………
प्रश्न 2.
अणुगति सिद्धान्त के अनुसार किसी पात्र में भरी गैस द्वारा पात्र की दीवारों पर आरोपित दाब की गणना कीजिये।
उत्तर:
आदर्श गैस का दाब
(Pressure of an Ideal Gas)
जब कोई गैस किसी बर्तन में बन्द कर दी जाती है तो वह बर्तन की दीवार पर दाब लगाती है। गैस के अणुगति मॉडल के अनुसार गैसदाब गैस के गतिमान अणुओं द्वारा बर्तन की दीवारों से टकराने के कारण उत्पन्न होता है। जब भी गैस का कोई अणु दीवार से टकराकर लौटता है, तो उनके संवेग में कुछ परिवर्तन होता है। संवेग संरक्षण सिद्धान्त के अनुसार यह परिवर्तन दीवार को हस्तान्तरित हो जाता है। गति के द्वितीय नियम से संवेग परिवर्तन की दर दीवार पर लगने वाले बल के बराबर होती है क्योंकि गैस में असंख्य अणु निरन्तर एक के बाद एक दीवार से टकराते हैं। दीवार पर लगा बल स्थायी होता है। दीवार के इकाई क्षेत्रफल पर आरोपित बल ही गैस का दाब होता है।
दाब का व्यंजक (Formula for the Pressure)-माना गैस एक घनाकार पात्र में है। जिसकी प्रत्येक भुजा की लम्बाई l है। गैस के अणुओं की संख्या n तथा प्रत्येक अणु पात्र के सापेक्ष C1, C2, C3,……… Cn, वेगों से यादृच्छिक गति कर रहे हैं। चित्र में निर्देशांक अक्षों को घन की भुजाओं के समान्तर लिया गया है।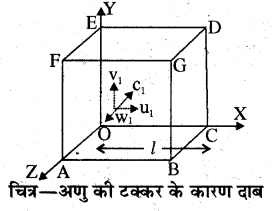
X, Y तथा Z अक्षों के अनुदिश वेगों के घटक क्रमशः u, v तथा w हैं। अतः C1 के.घटक u1, v1, w1, C2) के घटक u2, v2, w2,…… इत्यादि हैं। इस प्रकार से
C1 के लिये C12 = u12 + v12 + w12 ……… (1)
C2 के लिये C22 = u22 +v22 + w22
Cn के लिये Cn2 = un2 + vn2 + wn2 ………… (2)
अणु के संवेग में परिवर्तन = -mu1 – mu1 = -2mu1
∴ अणु के संवेग में परिवर्तन = -2mu1 ………….. (3)
यह संवेग का परिवर्तन संवेग संरक्षण के अनुसार दीवार को स्थानान्तरित संवेग के बराबर होगा। यही अणु दीवार OAFE से प्रतिक्षिप्त होकर तब तक 2l दूरी u1 वेग से तय करके पुनः दीवार CBGD पर पहुँचेगा।
एक टक्कर में लगा समय = (frac{2 l}{mathrm{u}_{1}}) सेकण्ड
∴ 1 सेकण्ड में किसी दीवार पर टक्करों की संख्या
(=frac{mathrm{u}_{1}}{2 l})
अतः एक अणु द्वारा एक सेकण्ड में होने वाली टक्करों के कारण संवेग में परिवर्तन का मान एक टक्कर में संवेग में परिवर्तन व कुल टक्करों की संख्या के गुणनफल (left(frac{2 m mathbf{u}_{1} times mathbf{u}_{1}}{2 l}right)) के बराबर होगा।
चूँकि संवेग में परिवर्तन की दर दीवार पर लगने वाले बल के । बराबर होगी, अतः अणुओं की टक्करों के कारण दीवार पर लगाया गया बल
(=frac{m mathbf{u}_{1}^{2}}{l})
अब इसी प्रकार पर सभी अणुओं द्वारा लगाया गया कुल बल होगा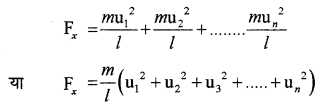
चूँकि एकांक क्षेत्रफल पर लगने वाला बल उस पर लग रहे दाब के बराबर होता है, अतः दीवार CBGD लगने वाला दाब होगा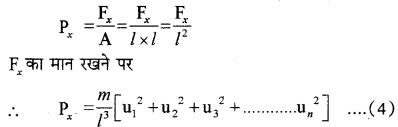
इसी प्रकार से अन्य दीवारों DEFG तथा ABGF पर लगने वाले दाब होंगे

प्रश्न 3.
स्वतंत्रता की कोटि से क्या अभिप्राय है? एकपरमाणुक, द्विपरमाणुक व बहुपरमाणुक गैस की विशिष्ट ऊष्माओं की व्याख्या कीजिये।
उत्तर:
कोई कण या अणु या परमाणु जितनी दिशाओं में स्वतंत्रतापूर्वक गति कर सकता है, दिशाओं की उसे संख्या को कण की स्वतंत्रता कोटि कहते हैं।
उदाहरण के लिए, किसी छड़ में पिरोया हुआ छल्ला केवल छड़ की लम्बाई के अनुदिश ही चलने को स्वतंत्र है, अतः छल्ले की स्वतंत्रता कोटि एक होगी। इसी प्रकार कैरमबोर्ड पर चलने वाली गोटियाँ केवल उसकी लम्बाई व चौड़ाई तल में चल सकती हैं। अतः स्वतंत्रता कोटि दो होगी। आकाश में उड़ने वाले गुब्बारे की स्वतंत्रता कोटि तीन होगी क्योंकि वह तीनों (x, y व z) दिशाओं में उड़ने को स्वतंत्र है।
इसके अतिरिक्त किसी निकाय की सम्पूर्ण अवस्था या उसकी स्थिति तथा विन्यास को प्रदर्शित करने के लिए जितने स्वतंत्र निर्देशांकों या चरों की आवश्यकता होती है, उनकी संख्या को स्वतंत्रता कोटि कहते हैं।
स्वतंत्रता की कोटियाँ तीन प्रकार की होती हैं
(a) स्थानान्तरण की स्वतंत्रता की कोटियाँ
(b) घूर्णन की स्वतंत्रता की कोटियाँ
(c) कम्पन की स्वतंत्रता की कोटियाँ
(a) स्थानान्तरण की स्वतंत्रता की कोटियाँ (Degrees of Freedom Translation Motion)- स्थानान्तरण की स्वतंत्रता की कोटियाँ अणु की स्थानान्तरीय या रेखीय गति के कारण उत्पन्न होती हैं। इनकी अधिकतम तीन होती हैं। ये सामान्य ताप पर उपस्थित होती हैं।
(b) घूर्णन की स्वतंत्रता की कोटियाँ (Degrees of Freedom of Rotation Motion)- घूर्णन की स्वतंत्रता की कोटि अणु के द्रव्यमान केन्द्र से पारित अक्ष के सापेक्ष घूर्णन गति के कारण होती है। इनकी संख्या अणु की संरचना पर निर्भर करती है। यह सामान्य ताप पर उपस्थित रहती हैं।
(c) कम्पन की स्वतंत्रता की कोटियाँ (Degrees of Freedom of Vibrational Motion)- कम्पन की स्वतंत्रता की कोटि अणुओं के कम्पनों के कारण होती है। इनकी संख्या भी अणु की संरचना पर निर्भर करती है। ये साधारणतया सामान्य ताप पर उपस्थित न होकर उच्च ताप पर उपस्थित होती हैं। इसमें प्रत्येक कम्पन तरीके के लिए कम्पन की स्वतंत्रता की कोटि दो होती हैं। इसमें से एक स्थितिज ऊर्जा व एक गतिज ऊर्जा के संगत।
माना N कणों से निर्मित एक निकाय में कणों के मध्य में स्वतन्त्र सम्बन्ध हो, तो निकाय की स्वतन्त्रता की कोटियाँ होंगी
f = 3N – k
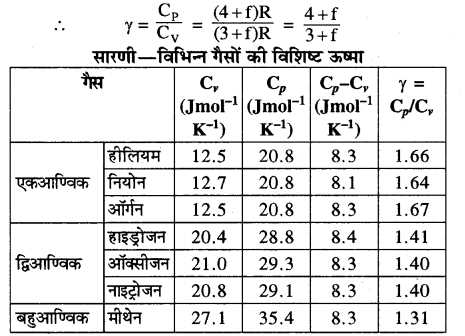
एक परमाणुक गैस की विशिष्ट ऊष्मा (Specific heat of Monoatomic Gas)- [उदाहरण-निष्क्रिय गैसें, हीलियम, नीओन आदि]
हम जानते हैं एक ग्राम मोल गैस के अणुओं की कुल ऊर्जा होगी
यहाँ J जूल नियतांक या ऊष्मा का यांत्रिक तुल्यांक कहलाता है। इसका मान 4.18 जूल/कैलोरी होता है। चूँकि (frac{mathrm{d} mathrm{U}}{mathrm{dT}}) एक ग्राम अणु गैस की नियत आयतन पर विशिष्ट ऊष्मा होती है। इसलिए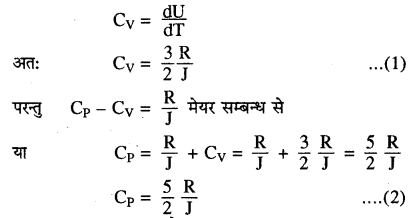
समीकरण (1) व (2) से स्पष्ट है कि गैस की मोलर विशिष्ट ऊष्माएँ CP व CV ताप पर निर्भर नहीं करती हैं। |
यहाँ (frac{C_{P}}{C_{V}}=frac{5}{3}) = 1.67
अर्थात् एकपरमाणुक गैस की मोलर विशिष्ट ऊष्माओं की निष्पत्ति (frac{C_{p}}{C_{v}}) = γ का मान 1.67 के बराबर होता है।
द्विपरमाणुक गैस की विशिष्ट ऊष्मा (Specific Heat of a Diatomic Gas)- [उदाहरण-हाइड्रोजन, नाइट्रोजन, क्लोरीन आदि ]
हम जानते हैं एक ग्राम मोल द्विपरमाणुक गैस के अणुओं की कुल ऊर्जा U = (frac{1}{2}) fRT
समीकरण (1) तथा (2) से स्पष्ट है कि गैस की मोलर विशिष्ट ऊष्माएँ CP व CV ताप पर निर्भर नहीं करती हैं।
(frac{C_{P}}{C_{V}}=frac{7}{5}) = 1.4
अर्थात् द्विपरमाणुक गैस की मोलर विशिष्ट ऊष्माओं की निष्पत्ति ? का मान 1.4 के बराबर होता है।
त्रिपरमाणुक गैस की विशिष्ट ऊष्मा (Specific Heat of a Triatomic Gas)
(A) अरेखीय अणुओं वाली त्रिपरमाणुक गैस के लिए स्वतंत्रता की कोटियाँ (f) = 6 [उदाहरण-H2O अणु]
1 ग्राम मोल गैस के अणुओं की कुल ऊर्जा
लेकिन (frac{C_{P}}{C_{V}}) = γ
∴ γ = 1.33
(B) रेखीय अणुओं वाली त्रिपरमाणुक गैस के लिए [उदाहरण– कार्बन डाईऑक्साइड]
f = 7
बहुपरमाणुक गैसों की विशिष्ट ऊष्मा (Specific Heat of Polyatomic Gases)
व्यापक रूप में किसी बहुपरमाणुक अणु में 3 स्थानान्तरीय, 3 घूर्णी स्वातंत्र्य कोटि एवं कुछ निश्चित संख्या (f) के कम्पन रूप होते हैं। ऊर्जा समविभाजन के नियमानुसार यह सुगमता से समझा जा सकता है कि इस प्रकार की गैस के 1 मोल की कुल आन्तरिक ऊर्जा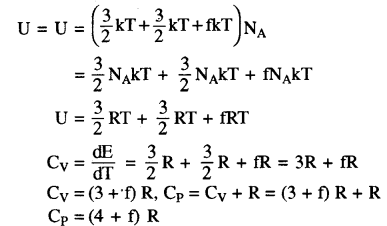
प्रश्न 4.
आदर्श गैसों व वास्तविक गैसों में अन्तर स्पष्ट कीजिये।
उत्तर:
वास्तविक गैसों के अणुओं में अन्तराण्विक बल उपस्थित रहते हैं। तथा उनके अणुओं का भी कुछ निश्चित आयतन होता है। इन गैसों की अवस्था समीकरण को (left(mathrm{P}+n^{2} frac{a}{mathrm{v}^{2}}right))(V – nb) = nRT से प्रदर्शित किया जाता है। (विस्तृत जानकारी के लिए 14.4 देखें)। यहाँ प्रतीकों के सामान्य अर्थ हैं। वास्तविक गैसों के विपरीत यदि पात्र में उपस्थित अणुओं के मध्य अन्तराण्विक बलों को नगण्य मान लें तथा अणुओं का आयतन भी पात्र की तुलना में नगण्य मान लें तो ऐसी गैस को आदर्श गैस कहते हैं। आदर्श गैस का समीकरण PV = nRT है। किसी भी वास्तविक गैस को निम्न दाब तथा उच्च ताप पर आदर्श गैस माना जा सकता है।
गैसों के अवस्था समीकरण PV = RT के द्वारा आदर्श गैस के व्यवहार की व्याख्या की जा सकती है परन्तु ऐण्ड्रयूज और एमागाट के प्रयोगों से यह निष्कर्ष निकलता है कि यह समीकरण पूर्णरूप से सही नहीं है। साथ ही गैसों के निर्बाध प्रसरण में भी ताप में कमी से यह निष्कर्ष निकलता है कि गैसों की अभिधारणाएँ पूर्ण रूप से सही नहीं हैं। वास्तव में गैसों में अन्तर-अणुक बल होते हैं तथा गैसों के अणु कुछ आयतन अवश्य घेरते हैं । यद्यपि अधिक ताप तथा कम दाब पर गैसों के लिए ये अभिधारणाएँ काफी सीमा तक सही हैं, परन्तु कम ताप और अधिक दाब पर इन अभिधारणाओं से विसंगति हो जाती है। अर्थात् गैसों के अणुओं के मध्य अन्तर-अणुक बल तथा उनके द्वारा घेरा गया कुल आयतन नगण्य नहीं रहता।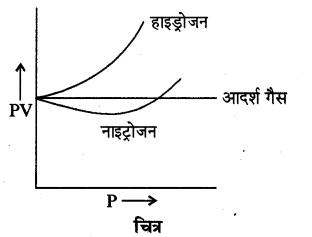
उच्च दाबे तथा निम्न ताप पर वास्तविक गैसों में PV का मान स्थिर नहीं रहता जैसा कि चित्र में दर्शाया गया है। हाइड्रोजन के लिए P का मान बढ़ने पर PV का मान बढ़ता है जबकि नाइट्रोजन के लिए P का मान बढ़ने पर पहले PV का मान घटता है फिर बढ़ने लगता है। इस प्रकार हम देखते हैं कि दोनों गैसों के व्यवहार में काफी अन्तर है। सन् 1876 में वान्डरवाल ने वास्तविक गैसों से आदर्श गैस से विचलन के निम्न दो मुख्य कारण दिये, जो कि निम्न हैं
(i) अणुओं के अशून्य आकार के कारण आयतन में संशोधन-आदर्श गैस में अणुओं को बिन्दु मात्र माना जाता है। इस कारण अणुओं के कुल आयतन को नगण्य मानते हुए गैस का आयतन बर्तन का आयतन ही माना जाता है। परन्तु वास्तविक गैसों में अणुओं का आकार नगण्य नहीं माना जा सकता है।
वास्तविक गैस के लिए अणु का आकार लगभग 10-10 मीटर की कोटि का होता है जबकि गैस के दो अणुओं के मध्य दूरी 10-9 मीटर कोटि की होती है। यदि गैस का आयतन V है तो इस आयतन का कुछ भाग तो अणु ही घेर लेते हैं। इस कारण अणुओं के प्रभावी आयतन को गैस के आयतन V में घटाना होगा जो कि (b) अणुओं के कुल आयतन का चार गुना होगा। इसे निम्न प्रकार समझाया जा सकता है।
माना कि r अणु का अर्थ व्यास तथा n अणुओं की संख्या बर्तन में दो अणुओं के लिए अउपलब्धता
अन्तराण्विक अन्योन्य क्रिया- आदर्श गैस में अणुओं के मध्य किसी प्रकार के आकर्षण बल या प्रतिकर्षण बल नहीं होते हैं। जबकि वास्तविक गैसों में अणुओं के मध्य अन्तराण्विक बल होते हैं, जिन्हें वान्डरवाल बल भी कहते हैं। उच्च ताप व निम्न दाब पर इनके प्रभाव को नगण्य माना जा सकता है। परन्तु निम्न ताप उच्च दाब पर इनका प्रभाव नगण्य नहीं होता है। इस कारण गैस का वास्तविक दाब प्रेक्षित दाब से अधिक होगा। इसे निम्न प्रकार समझाया जा सकता है
माना कि किसी बंद पात्र में गैस के n अणु भरे हैं। जो अणु पात्र में पूर्ण रूप से अन्दर हैं उन पर चारों ओर से अणुओं द्वारा समान रूप से आकर्षण बल लगेगा, इस कारण ऐसे अणुओं पर परिणामी अन्तराण्विक बल शून्य होगा। परन्तु वे अणु जो कि दीवार के समीप हैं, इन पर परिणामी अन्तराण्विक बल शून्य नहीं होगा परन्तु अन्दर की ओर कार्य करेगा। इस अन्दर की ओर खिंचाव के कारण दीवार से टकराते समय इन अणुओं के संवेग में कुछ कमी आ जाती है। इस कारण अणु दीवार पर उतना बल नहीं लगा पाते जितना कि वे अन्तराण्विक बलों की अनुपस्थिति में कर पाते। इस कमी को निम्न प्रकार से समझाया जा सकता है
n = पात्र में कुल अणुओं की संख्या
n1 = दीवार से टकराने वाले अणुओं की संख्या
n2 = दीवार से टकराने वाले अणुओं को भीतर खींचने वाले
अणुओं की संख्या
इस कारण दाब में कमी Pin
Pin ∝ n1
Pin ∝ n2
परन्तु
n1 ∝ n
n2 ∝ n
∴ Pin ∝ n2
n ∝ (frac{1}{V})
∴ Pin ∝ (frac{1}{mathrm{V}^{2}})
या Pin = (frac{a}{V^{2}})
यहाँ पर वान्डरवाल नियतांक है। इस कारणं गैस का वास्तविक दाब
P’ = (P + Pin)
= (left(P+frac{a}{V^{2}}right))
अतः एक ग्राम अणु भार के गैस का वास्तविक गैस समीकरण होगा
P’V’ = RT
(left(P+frac{a}{V^{2}}right)) (V – b) = RT
इसे वान्डरवाल गैस समीकरण भी कहते हैं।
गैस के n मोल का समीकरण निम्न होगा
(left(mathrm{P}+frac{a n^{2}}{mathrm{V}^{2}}right)) (V – nb) = nRT
प्रश्न 5.
आदर्श गैस की गतिज ऊर्जा व ताप के मध्य सम्बन्ध की व्युत्पत्ति कीजिये।
उत्तर:
यहाँ m गैस के एक अणु का द्रव्यमान, N अणुओं की संख्या तथा NA आवोगाद्रो संख्या है।
गैस के 1 ग्राम अणु में अणुओं की संख्या NA = 6.023 × 1023 प्रति ग्राम मोल होती है। इस संख्या को ही आवोगाद्रो संख्या कहते हैं।
एक मोल गैस के लिए M = MA
अतः एक मोल गैस की माध्य गतिज ऊर्जा
= (frac{1}{2} mathbf{M}_{mathrm{A}} overline{mathrm{C}^{2}}) ………..(2)
दाब व गैस के अणुओं की माध्य गतिज ऊर्जा में सम्बन्ध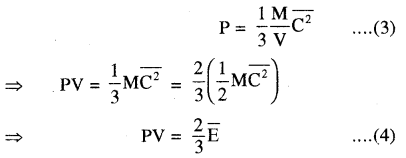
यहाँ (overline{mathrm{E}}=frac{1}{2} mathrm{MC}^{2}) गैस की माध्य गतिज ऊर्जा है।
समीकरण (4) से P = (frac{2}{3} frac{overline{mathrm{E}}}{mathrm{V}})
अतः इकाई आयतन वाली गैस की औसत गतिज ऊर्जा का (frac{2}{3}) भाग कुल दाब के बराबर होता है।
माध्य गतिज ऊर्जा निम्न परिस्थितियों में ज्ञात की जा सकती है
(i) औसत ऊर्जा (Average energy)-किसी एक मोल गैस की माध्य गतिज ऊर्जा के मान को उसकी औसत ऊर्जा या माध्य ऊर्जा कहते हैं।
समीकरण (3) से
(overline{mathrm{E}}=frac{3}{2} mathrm{PV}=frac{3}{2} mathrm{RT})
जहाँ R गैस नियतांक है तथा इसका मान 8.31 जूल/मोल केल्विन होता है।
(ii) प्रति ग्राम अथवा प्रति किलोग्राम माध्य गतिज ऊर्जा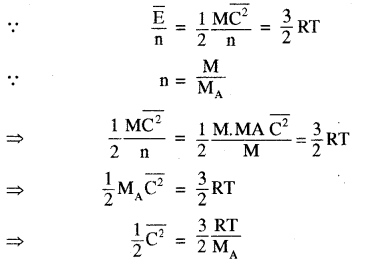
अतः प्रति ग्राम अथवा प्रति किलोग्राम माध्य गतिज ऊर्जा
यह बोल्ट्रजमान नियतांक (Boltazmann Constant) कहलाता है, जिसका मान 1.38 x 10-23 जूल/केल्विन होता है। अतः प्रतिअणु माध्य गतिज ऊर्जा = (frac{3}{2}) KT अर्थात् एक ही ताप पर भिन्न-भिन्न गैसों के लिए प्रति अणु औसत गतिज ऊर्जा समान होती है तथा यह गैस के परमताप के समानुपाती होती है।
अर्थात् प्रतिअणु माध्य गतिज ऊर्जा ताप का मापक है। परम शून्य ताप पर (T = 0) गैस के अणुओं की ऊर्जा शून्य हो जायेगी एवं अणु गतिविहीन हो जायेंगे।
RBSE Class 11 Physics Chapter 14 आंकिक प्रश्न
प्रश्न 1.
300 K ताप पर किसी गैस के लिये वर्ग माध्य मूल वेग की गणना कीजिये यदि गैस का अणुभार 221 व R = 8.3 Jmol-1K-1 है।
हल:
हम जानते हैं कि गैस का वर्गमाध्य मूल वेग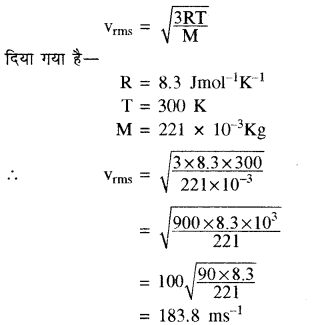
प्रश्न 2.
यदि NTP पर नाइट्रोजन का घनत्व 1.25 gmL-1 हो तो 0 तथा 20°C ताप पर इस गैस के अणुओं का वर्ग माध्य मूल वेग ज्ञात करो।
हल:
हम जानते हैं कि गैस के अणुओं का वर्ग माध्य मूल वेग
प्रश्न 3.
किस ताप पर एक अणु की गतिज ऊर्जा 1.0 ev होगी? (kB = 1.38 × 10-23JK-1)
हल:
हम जानते हैं कि गैस के एक अणु की गतिज ऊर्जा
E = (frac{3}{2}) kT
दिया गया है
E = 1.0eV = 1 × 1.6 × 10-19J
k = 1.38 × 10-23JK-1
∴ T = (frac{2}{3} frac{mathrm{E}}{mathrm{k}})
= (frac{2}{3} times frac{1.6 times 10^{-19}}{1.38 times 10^{-23}})
= (frac{3.2 times 10^{4}}{4.14} mathrm{K})
= 7730 K
प्रश्न 4.
किसी गैस के लिये वाण्डरवाल नियतांक a = 1.32 b = 3.12 × 10-2 है तब वह ताप ज्ञात करो जिस पर 5 am दाब व 5 mol गैस का आयतन 20 L हो। पुनः गैस दाब ज्ञात करो जब आयतन 2 L हो जाये। (R = 8.314 Jmol-1K-1)
हल:
दिया गया है a = 1.32 L2 atm mol-2 = 1.32 × 10-6 m2 atm mol-2
b = 3.12 × 10-2 L mol-1
n = 5 mol
V = 20 L
P = 5 atm
(1) वाण्डरवाल गैस समीकरण से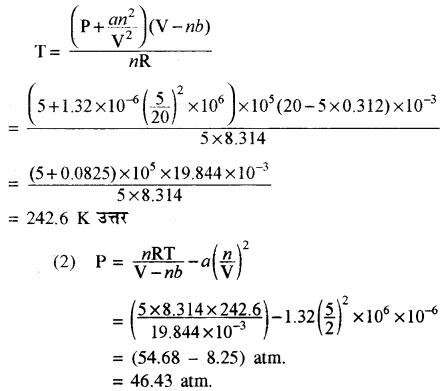
प्रश्न 5.
ऑक्सीजन गैस के लिए वाण्डरवाल नियंताक a = 1.32 व b = 3.12 × 10-2 है। यदि गैस का ताप 300 K है तब इसका आयतन 1.2L mol-1 हो तो गैस के दाब की गणना करो। (R = 8.314 Jmol-1K-1)
हल:
हम जानते हैं कि वाण्डरवाल समीकरण से दाब
P = (frac{mathrm{RT}}{(mathrm{V}-b)}-frac{a}{mathrm{V}^{2}})
दिया गया है
a = 1.32 L2 atm mol-2
b = 1.32 × 10-6 m2 atm mol-2
b = 3.12 × 10-2L mol-1
= 3.12 × 10-5 m3 mol-1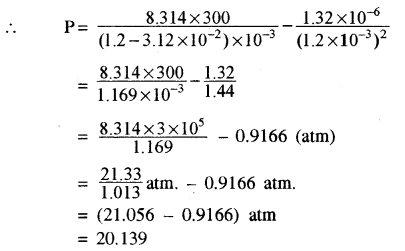
प्रश्न 6.
किसी फ्लास्क में आर्गन व क्लोरीन गैस भरी हुई है। जिनके द्रव्यमान के अनुपात 2:1 व मिश्रण का ताप 27°C है। दोनों गैसों के लिये निम्न की गणना कीजिये
(i) प्रति अणु की औसत गतिज ऊर्जा।
(ii) अणुओं के वर्ग माध्य मूल वेग का अनुपात। यहाँ आर्गन का रमाणु द्रव्यमान 39.94 वे क्लोरीन अणु का द्रव्यमान 70.94 है।
हल:
दिया है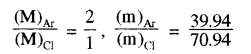
मिश्रण का ताप T = 27°C = 27 + 273 = 300 K
चूँकि गैस की प्रति अणु औसत गतिज ऊर्जा
(frac{1}{2} mathrm{m} overline{mathrm{C}^{2}}=frac{3}{2} mathrm{kT}) (जहाँ k = बोल्ट्ज मान नियतांक है) अतः गैस की प्रति अणु औसत गतिज ऊर्जा केवल ताप पर निर्भर करती है तथा मिश्रण की दोनों गैसों का ताप समान है। अतः ।
(i) प्रति अणु की औसत गतिज ऊर्जा का अनुपात समान होगा अर्थात् 1 : 1
(ii) चूँकि समान ताप पर दो भिन्न-भिन्न गैसों के अणुओं की वर्ग माध्य मूल चालों का अनुपात उनके अणुभारों के वर्ग मूलों के व्युत्क्रमानुपाती होता है।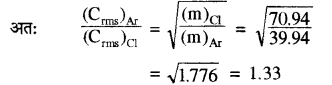
प्रश्न 7.
373 K ताप पर जलवाष्प में जल के अणु के माध्य मुक्त पथ की गणना करो यदि जल के अणुओं का व्यास 2 × 10-10 m है।
हल:
हम जानते हैं कि NTP पर सभी गैसों के 22.4 लीटर आयतन में अणुओं की संख्या 6.02 × 1023 होती है।
अतः
∴ n1 = (frac{6.02 times 10^{23}}{22.4 times 10^{-3}})
= 2.7 × 1025 m-3
तथा P = nKT
n ∝ (frac{1}{mathrm{T}})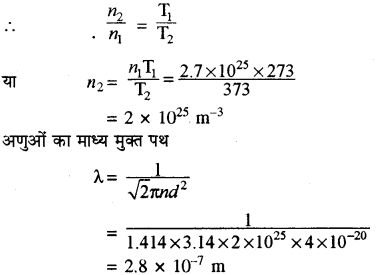
प्रश्न 8.
यदि वायु का ताप 127 से 227°C हो जाये तो उसके अणुओं की गतिज ऊर्जा किस अनुपात में बढ़ जायेगी?
हल:
हम जानते हैं कि अणुओं की माध्य गतिज ऊर्जा = (frac{3}{2}) kT होती है।
∴ Ε ∝ T
(frac{E_{2}}{E_{1}}=frac{T_{2}}{T_{1}})
दिया गया है
T1 = 127 + 273 = 400 K
T2 = 227 + 273 = 500 K
∴ (frac{mathrm{E}_{2}}{mathrm{E}_{1}}=frac{500}{400})
= 5 : 4
प्रश्न 9.
यदि 1 mol एक परमाणुक गैस (γ = (frac{5}{3})) को 1 mol द्विपरमाणुक गैस (γ = (frac{7}{5})) में मिश्रित किया जाये तो मिश्रण के γ की गणना कीजिये। जहाँ γ = CP/CV
हल:
हम जानते हैं कि गैसों के मिश्रण के λ का सूत्र होता है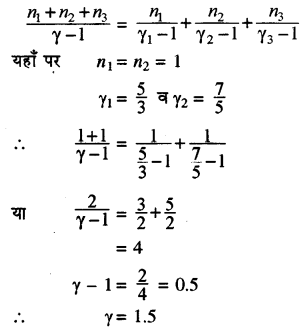
प्रश्न 10.
एक पात्र में 16 gm हीलियम व 16 gm ऑक्सीजन का मिश्रण है तब मिश्रण के γ की गणना करो।
हल:
हम जानते हैं कि मिश्रण के लिए γ का सूत्र है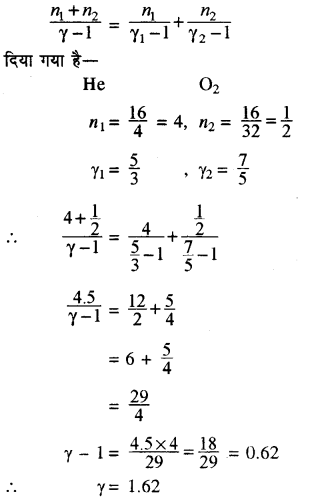
प्रश्न 11.
किसी बर्तन में 27°C पर 0.014 kg नाइट्रोजन भरी है। इसके अणुओं का वर्ग-मध्य मूल वेग दुगुना करने के लिए गैस को कितनी ऊष्मा देनी होगी? [kB = 1.38 × 10-23 JK-1 तथा N = 6 × 1026 (kg-mol)-1]
हल:
हम जानते हैं कि द्विपरमाणु गैस ऊर्जा E = (frac{5}{2}) kT प्रति अणु
∴ कुल ऊर्जा में अन्तर
ΔE = (frac{5}{2}) k(T2 – T1)n
दिया गया है- k = 1.38 × 10-23 JK
n = (frac{6 times 10^{26}}{28} times 0.014)
= 3 × 1023
T2 = 300 × 4 = 1200, T1 = 300
∴ ΔE = (frac{5}{2}) × 1.38 × 10-23 × (1200 – 300) × 3 × 1023
= 2.5 × 1.38 × 900 × 3
= 2.5 × 1.38 × 2700 J
= 9315 J
28
All Chapter RBSE Solutions For Class 12 Physics Hindi Medium
—————————————————————————–
All Subject RBSE Solutions For Class 11 Hindi Medium
*************************************************
————————————————————
All Chapter RBSE Solutions For Class 11 physics Hindi Medium
All Subject RBSE Solutions For Class 11 Hindi Medium
Remark:
हम उम्मीद रखते है कि यह RBSE Class 11 physics Solutions in Hindi आपकी स्टडी में उपयोगी साबित हुए होंगे | अगर आप लोगो को इससे रिलेटेड कोई भी किसी भी प्रकार का डॉउट हो तो कमेंट बॉक्स में कमेंट करके पूंछ सकते है |
यदि इन solutions से आपको हेल्प मिली हो तो आप इन्हे अपने Classmates & Friends के साथ शेयर कर सकते है और HindiLearning.in को सोशल मीडिया में शेयर कर सकते है, जिससे हमारा मोटिवेशन बढ़ेगा और हम आप लोगो के लिए ऐसे ही और मैटेरियल अपलोड कर पाएंगे |
आपके भविष्य के लिए शुभकामनाएं!!